题目内容
已知双曲线方程C：
-
=1（b＞a＞0）的离心率为e1，其实轴与虚轴的四个顶点和椭圆的四个顶点重合，椭圆G的离心率为e2，一定有（ ）
| x2 |
| a2 |
| y2 |
| b2 |
分析：根据0＜a＜b，椭圆G的焦点在y轴上，写出其标准方程求出e22=
，e12=
，依次验证即可．
| b2-a2 |
| b2 |
| a2+b2 |
| a2 |
解答：解：∵0＜a＜b，∴椭圆G的焦点在y轴上，其标准方程是：
+
=1，
∴e22=
，而e12=
，
∴e12+e22=
+
=
=2+
•
=2+e12•e22．
故选C．
| y2 |
| b2 |
| x2 |
| a2 |
∴e22=
| b2-a2 |
| b2 |
| a2+b2 |
| a2 |
∴e12+e22=
| b2-a2 |
| b2 |
| a2+b2 |
| a2 |
| 2a2b2+b4-a4 |
| a2b2 |
| a2+b2 |
| a2 |
| b2-a2 |
| b2 |
故选C．
点评：本题考查了双曲线与椭圆的简单性质，正确的求出椭圆的离心率是解答的关键．
练习册系列答案
相关题目
，椭圆C以该双曲线的焦点为顶点，顶点为焦点．
，b=1时，求椭圆C的方程；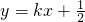
与y轴交于点P，与椭圆交与A，B两点，若O为坐标原点，△AOP与△BOP面积之比为2：1，求直线l的方程；
，椭圆方程
，A、D分别是双曲线和椭圆的右准线与x轴的交点，B、C分别为双曲线和椭圆的右顶点，O为坐标原点，且|OA|，|OB|，|OC|，|OD|成等比数列．