题目内容
已知双曲线方程为 ,椭圆C以该双曲线的焦点为顶点,顶点为焦点.
,椭圆C以该双曲线的焦点为顶点,顶点为焦点.
(1)当 ,b=1时,求椭圆C的方程;
,b=1时,求椭圆C的方程;
(2)在(1)的条件下,直线l: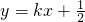 与y轴交于点P,与椭圆交与A,B两点,若O为坐标原点,△AOP与△BOP面积之比为2:1,求直线l的方程;
与y轴交于点P,与椭圆交与A,B两点,若O为坐标原点,△AOP与△BOP面积之比为2:1,求直线l的方程;
(3)若a=1,椭圆C与直线l':y=x+5有公共点,求该椭圆的长轴长的最小值.
解:(1)设双曲线的焦点为(±c,0)(c>0),则椭圆C的方程为 ,其中c2=a2+b2
,其中c2=a2+b2
将 代入,可得椭圆C的方程为
代入,可得椭圆C的方程为 ;
;
(2)根据题意,设点A,B的坐标分别为(x1,y1),(x2,y2),则|x1|:|x2|=2:1,可知.
联立椭圆和直线的方程,得 ,消元得
,消元得 ,可知
,可知 ,
, ,即x1与x2异号,所以x1=-2x2.
,即x1与x2异号,所以x1=-2x2.
代入上式,得 ,消元,得
,消元,得 .
.
所以直线方程为
(3)联立椭圆和直线的方程,得方程组 ,其中c2=b2+1
,其中c2=b2+1
消去y,可得( +
+ )x2+
)x2+ +
+ -1=0
-1=0
∴△= ,
,
解得b2≥12,所以c2≥13,当且仅当 时长轴长最短,是
时长轴长最短,是 .
.
分析:(1)根据椭圆C以该双曲线的焦点为顶点,顶点为焦点,设椭圆方程,将 代入,可得椭圆C的方程;
代入,可得椭圆C的方程;
(2)根据题意,设点A,B的坐标分别为(x1,y1),(x2,y2),联立椭圆和直线的方程,利用韦达定理及x1=-2x2,即可求直线l的方程;
(3)联立椭圆和直线的方程,利用判别式大于等于0,即可求得结论.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.
 ,其中c2=a2+b2
,其中c2=a2+b2将
 代入,可得椭圆C的方程为
代入,可得椭圆C的方程为 ;
;(2)根据题意,设点A,B的坐标分别为(x1,y1),(x2,y2),则|x1|:|x2|=2:1,可知.
联立椭圆和直线的方程,得
 ,消元得
,消元得 ,可知
,可知 ,
, ,即x1与x2异号,所以x1=-2x2.
,即x1与x2异号,所以x1=-2x2.代入上式,得
 ,消元,得
,消元,得 .
.所以直线方程为

(3)联立椭圆和直线的方程,得方程组
 ,其中c2=b2+1
,其中c2=b2+1消去y,可得(
 +
+ )x2+
)x2+ +
+ -1=0
-1=0∴△=
 ,
,解得b2≥12,所以c2≥13,当且仅当
 时长轴长最短,是
时长轴长最短,是 .
.分析:(1)根据椭圆C以该双曲线的焦点为顶点,顶点为焦点,设椭圆方程,将
 代入,可得椭圆C的方程;
代入,可得椭圆C的方程;(2)根据题意,设点A,B的坐标分别为(x1,y1),(x2,y2),联立椭圆和直线的方程,利用韦达定理及x1=-2x2,即可求直线l的方程;
(3)联立椭圆和直线的方程,利用判别式大于等于0,即可求得结论.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: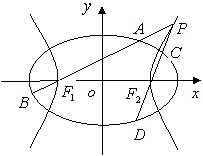 (Ⅰ)求椭圆和双曲线的标准方程;
(Ⅰ)求椭圆和双曲线的标准方程;  :
: 与双曲线
与双曲线 :
: 有相同的焦点
有相同的焦点 ,
, 是椭圆
是椭圆 的周长为
的周长为 ,求椭圆
,求椭圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 的距离为
的距离为 ,
, 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;
 :
: (
(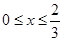 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧 :
: )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”.设过点
”.设过点 两点,
两点, ,
,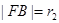 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.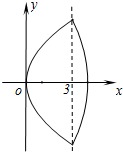 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: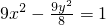 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;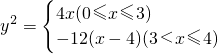 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 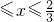 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: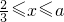 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.