题目内容
20．如图，在正方体ABCD-A1B1C1D1中，异面直线A1D与D1C所成的角为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 连结CB1，ABCD-A1B1C1D1是正方体，A1D∥B1C，异面直线A1D与D1C所成的角为∠B1CD1（或补角），连结B1D1，可得△B1D1C是等边三角形，可得∠B1CD1的大小．
解答 解：连结CB1，ABCD-A1B1C1D1是正方体，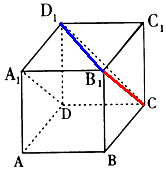
∴A1D∥B1C，
∴异面直线A1D与D1C所成的角为∠B1CD1（或补角），
连结B1D1，
可知B1D1=D1C=B1C，（三条边是平面的对角线）
∴△B1D1C是等边三角形，
∴∠B1CD1=60°，即异面直线A1D与D1C所成的角为60°．
故选：C．
点评 本题考查两条异面直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
10．如图是一个几何体的三视图，则这个几何体的体积为（ ）
| A． | 1 | B． | $\frac{4}{3}$ | C． | 3 | D． | 4 |
11．抛掷甲、乙两枚质地均匀且四面上分别标有1，2，3，4的正四面体，其底面落于桌面，记所得的数字分别为x，y，则$\frac{x}{y}$为整数的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
15．某校从参加高三年级学业水平考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为150分），其样本频率分布表如下（部分数据丢失）：
（Ⅰ）分别求出上表中的x；P1和P2的大小
（Ⅱ）估计成绩在120分以上学生的比例；
（Ⅲ）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[130，150）中选两位同学，共同帮助[30，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为135分，求甲、乙两同学恰好被安排在同一小组的概率．
| 分组 | 频数 | 频率 |
| [30，50） | 2 | 0.04 |
| [50，70） | 3 | 0.06 |
| [70，90） | 14 | P1 |
| [90，110） | 15 | 0.30 |
| [110，130） | x | P2 |
| [130，150） | 4 | 0.08 |
| 合计 | 50 | 1 |
（Ⅱ）估计成绩在120分以上学生的比例；
（Ⅲ）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[130，150）中选两位同学，共同帮助[30，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为135分，求甲、乙两同学恰好被安排在同一小组的概率．
12．从集合{1，2，3，5，11}中有放回地任取2次元素分别作为直线Ax+By=0中的A、B，则该直线恰好为坐标系角平分线的概率是（ ）
| A． | $\frac{1}{25}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
如图茎叶图记录了甲、乙两组各四名同学的植树棵数，乙组记录中有一个数据模糊，无法确认，在图中以x表示