Question

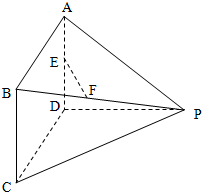（2012•威海二模）如图所示多面体中，AD⊥平面PDC，ABCD为平行四边形，E为AD的中点，F为线段BP上一点，∠CDP=120°，AD=3，AP=5，PC=2

7

．
（Ⅰ）若F为BP的中点，求证：EF∥平面PDC；
（Ⅱ）若BF=

1

3

BP，求直线AF与平面PBC所成角的正弦值．

Answer 1

分析：（Ⅰ）先证明四边形EFOD是平行四边形，再利用线面平行的判定定理证明EF∥平面PDC；
（Ⅱ）z轴建立空间直角坐标系，求得

AF

=(

2

3

，

2

3

3

，-1)，面PBC的法向量

n1

=(

3

2

，1，0)，利用向量的夹角公式，可求AF与平面PBC所成角的正弦值．

解答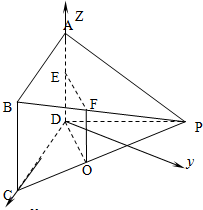：（Ⅰ）证明：取PC的中点为O，连FO，DO，
∵F，O分别为BP，PC的中点，
∴FO∥BC，且FO=

1

2

BC，
又ABCD为平行四边形，∴ED∥BC，且ED=

1

2

BC，
∴FO∥ED，且FO=ED
∴四边形EFOD是平行四边形------------------------------------（2分）
∴EF∥DO   
∵EF?平面PDC
∴EF∥平面PDC．---------------------------------------------（4分）
（Ⅱ）解：以DC为x轴，过D点做DC的垂线为y轴，DA为z轴建立空间直角坐标系，
则有D（0，0，0），C（2，0，0），B（2，0，3），P（-2，2

3

，0），A（0，0，3）-----（6分）
设F（x，y，z），则

BF

=(x-2，y，z-3)=

1

3

BP

=（-

4

3

，

2 3

3

，-1）
∴F（

2

3

，

2

3

3

，2），∴

AF

=(

2

3

，

2

3

3

，-1)-----------------------------（8分）
设平面PBC的法向量为

n1

=(x，y，z)
则

n1 • CB =0 n1 • PC =0

，即

3z=0 4x-2 3 y=0

，∴取y=1得

n1

=(

3

2

，1，0)--------------（10分）
∴cos＜

AF

，

n1

＞=

AF • n1

| AF || n1 |

=

2 3 × 3 2 + 2 3 3

5 3 × 7 2

=

6 21

35

∴AF与平面PBC所成角的正弦值为

6 21

35

．-------------------------（12分）

点评：本题考查线面平行，考查线面角，考查利用向量知识解决线面角问题，求得平面的法向量是关键．