题目内容
若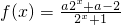 为奇函数.
为奇函数.
(1)判断它的单调性;
(2)求f(x)的值域.
解:(1)∵f(x)是奇函数,且在x=0处有定义,
∴f(0)=0,∴a=1,
∴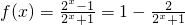
设x1<x2,则
∵x1<x2则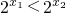 ,∴
,∴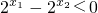 ,
,
∴f(x1)-f(x2)<0即f(x1)<f(x2)
故f(x)在R上递增.
(2)令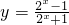 ,则
,则 .由于2x>0,所以
.由于2x>0,所以 ,解得-1<y<1
,解得-1<y<1
故f(x)的值域是(-1,1).
分析:(1)由f(x)是奇函数,可得f(0)=0,从而可求a及函数f(x),要证明函数f(x)单调性,只要任设x1<x2,然后比较f(x1)与f(x2)的大小即可
(2)利用反解法,由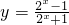 ,可得
,可得 .结合2x>0可求函数的值域
.结合2x>0可求函数的值域
点评:本题主要考查了利用奇函数的性质:奇函数得定义域内有0,则f(0)=0在求解函数解析式中的应用,应用该性质可以简化运算,反解法求解函数的值域常见在函数中含有2x,sinx,cosx等自身有范围限制得函数中.
∴f(0)=0,∴a=1,
∴
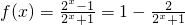
设x1<x2,则

∵x1<x2则
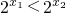 ,∴
,∴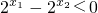 ,
,∴f(x1)-f(x2)<0即f(x1)<f(x2)
故f(x)在R上递增.
(2)令
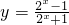 ,则
,则 .由于2x>0,所以
.由于2x>0,所以 ,解得-1<y<1
,解得-1<y<1故f(x)的值域是(-1,1).
分析:(1)由f(x)是奇函数,可得f(0)=0,从而可求a及函数f(x),要证明函数f(x)单调性,只要任设x1<x2,然后比较f(x1)与f(x2)的大小即可
(2)利用反解法,由
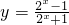 ,可得
,可得 .结合2x>0可求函数的值域
.结合2x>0可求函数的值域点评:本题主要考查了利用奇函数的性质:奇函数得定义域内有0,则f(0)=0在求解函数解析式中的应用,应用该性质可以简化运算,反解法求解函数的值域常见在函数中含有2x,sinx,cosx等自身有范围限制得函数中.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目