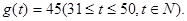题目内容
经市场调查,某种商品在120天内的日销售量和售价均为时间t(天)的函数,日销售量与时间的关系用图(1)的一条折线表示,售价与时间的关系用图(2)的一条折线表示.(1)写出图(1)表示的日销售量Q(千克)与时间t的函数关系式Q=g(t);
写出图(2)表示的售价(元/千克)与时间t的函数关系式P=f(t);
(2)求日销售额y(元)与时间t的函数关系,并求出日销售额最高的是哪一天?最高的销售额是多少?(注:日销售额=日销售量×售价)
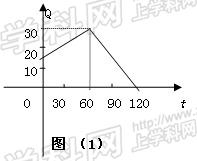
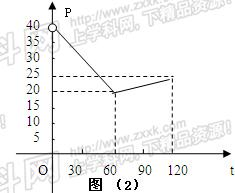
分析:(1)当0<t≤60时,直线过点(0,15),(60,30),求得函数g(t)的解析式;同理60<t≤120时,求得函数g(t),得分段函数g(t);同理可得:当0<t≤60时,函数f(t),当60<t≤120时,函数f(t);即分段函数f(t);
(2)当0<t≤60时,函数y=g(t)•f(t),计算最大值;当60<t≤120时,函数y=g(t)•f(t),计算最大值;综上得:分段函数y的最大值.
(2)当0<t≤60时,函数y=g(t)•f(t),计算最大值;当60<t≤120时,函数y=g(t)•f(t),计算最大值;综上得:分段函数y的最大值.
解答:解:(1)当0<t≤60时,直线过点(0,15),(60,30),所以函数g(t)=
t+15;
同理60<t≤120时,函数g(t)=-
t+60;
∴当日销售量Q与时间t的函数关系式Q=g(t)=
;
当0<t≤60时,函数f(t)=-
t+40;当60<t≤120时,函数f(t)=
t+15;
∴售价P与时间t的函数关系式P=f(t)=
;
(2)根据题意,当0<t≤60时,函数y=g(t)•f(t)=-
t2+5t+600,t=30时,y有最大值,是675;当60<t≤120时,函数y=g(t)•f(t)=-
t2 -
t+900,无最大值;
综上知:日销售额y与时间t的函数为:y=
;
且当t=30时,y最大,即在第30天的时候销售额最大,最高额为675元.
| 1 |
| 4 |
同理60<t≤120时,函数g(t)=-
| 1 |
| 2 |
∴当日销售量Q与时间t的函数关系式Q=g(t)=
|
当0<t≤60时,函数f(t)=-
| 1 |
| 3 |
| 1 |
| 12 |
∴售价P与时间t的函数关系式P=f(t)=
|
(2)根据题意,当0<t≤60时,函数y=g(t)•f(t)=-
| 1 |
| 12 |
| 1 |
| 24 |
| 5 |
| 2 |
综上知:日销售额y与时间t的函数为:y=
|
且当t=30时,y最大,即在第30天的时候销售额最大,最高额为675元.
点评:本题利用图象考查了分段函数的应用;利用图象求函数解析式时,要注意图象上的关键点,通过关键点的坐标,可得出所求的解析式.

练习册系列答案
相关题目


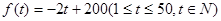 。前30天价格为
。前30天价格为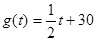
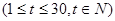 ,后20天价格为
,后20天价格为