题目内容
求证关于x的方程x2+2bx+1=0有两个负实根的充要条件是b≥1.
证明:充分性:∵b≥1,∴Δ=4b2-4≥0,
∴方程x2+2bx+1=0有实根并设为x1和x2,?
由韦达定理知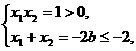 ∴x1<0,x2<0,即两根为负实数.?
∴x1<0,x2<0,即两根为负实数.?
必要性:∵x2+2bx+1=0的两实根均为负,?
且x1·x2=1,
∴2b=-(x1+x2)=-(x1+![]() )=(-x1)+
)=(-x1)+![]()
∵-x1>0,∴(-x1)+![]() ≥2,?
≥2,?
即2b≥2,∴b≥1.
综上,方程x2+2bx+1有两负根的充要条件是b≥1.

练习册系列答案
相关题目