题目内容
求证:关于x的方程x2+2ax+b=0有实数根,且两根均小于2的充分但不必要条件是a≥2且|b|≤4.
证明:∵a≥2,|b|≤4,∴a2≥4≥b.
∴Δ=4(a2-b)≥0.
∴方程x2+2ax+b=0有实根.
又∵![]()
∴(x1-2)+(x2-2)=(x1+x2)-4=-2a-4≤-4-4=-8<0.
而(x1-2)(x2-2)=x1x2-2(x1+x2)+4=b+4a+4≥-4+8+4=8>0,
∴
由以上知,“a≥2且|b|≤4”方程有实数根且两根均小于2.
再验证条件不必要:取x2-x=0的两根为x1=0,x2=1,则方程的两根均小于2,而a=-![]() <2,
<2,
∴“方程的两根小于2”![]() “a≥2且|b|≤4”.
“a≥2且|b|≤4”.
综上,a≥2且|b|≤4是方程有实数根且两根均小于2的充分但不必要条件.

练习册系列答案
相关题目
 .
.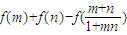 的值;
的值;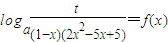 在x∈[0,1)上有实数解,求实数t的取值范围.
在x∈[0,1)上有实数解,求实数t的取值范围.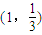 ,求证:
,求证: .
.