题目内容
设0<α<π,且函数f(x)=sin(x+α)+cos(x-α)是偶函数,则α?的值为________.
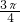
分析:从偶函数的定义入手,注意适当变形,通过待定系数法求解.
解答:∵f(-x)=sin(-x+α)+cos(-x-α)=sinαcosx-cosαsinx+cosxcosα-sinxsinα=f(x)=sinxcosα+cosxsinα+cosxcosα+sinxsinα
∴-cosαsinx-sinxsinα=sinxcosα+sinxsinα
∴-2sinxcosα=2sinxsinα
∴sinx(sinα+cosα)=0
∴α=(2k+1)π+
 ,k∈Z因为0<α<π,所以α=
,k∈Z因为0<α<π,所以α=
故答案为:
 .
.点评:本题通过偶函数来考查待定系数法求参数的值,还涉及到两角和与差的三角函数公式的正用.注意角的范围.

练习册系列答案
相关题目
设0<a<1,对于函数f(x)=
(0<x<π),下列结论正确的是( )
| sinx+a |
| sinx |
| A、有最大值而无最小值 |
| B、有最小值而无最大值 |
| C、有最大值且有最小值 |
| D、既无最大值又无最小值 |
 已知函数
已知函数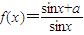 (0<x<π),下列结论正确的是( )
(0<x<π),下列结论正确的是( )