题目内容
设0<a<1,对于函数f(x)=
(0<x<π),下列结论正确的是( )
| sinx+a |
| sinx |
| A、有最大值而无最小值 |
| B、有最小值而无最大值 |
| C、有最大值且有最小值 |
| D、既无最大值又无最小值 |
分析:函数中出现的相同部分设成一个未知数,研究函数的单调性求值域
解答:解:令t=sinx,t∈(0,1],
则函数f(x)=
(0<x<π)的值域为函数y=1+
,t∈(0,1]的值域,
又a>0,
所以y=1+
,t∈(0,1]是一个减函减,
故选B.
则函数f(x)=
| sinx+a |
| sinx |
| a |
| t |
又a>0,
所以y=1+
| a |
| t |
故选B.
点评:通过换元,将三角函数转化成熟悉的代数函数,注意换元时新变量的范围.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 ;
;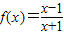 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.