题目内容
已知函数
，若实数x0是函数y=f（x）的零点，且0＜x1＜x0，则f（x1）
- A.大于0
- B.等于0
- C.小于0
- D.不大于0
A
分析：根据函数，利用指数函数和复合函数判断出它的单调性，根据实数x0是函数y=f（x）的零点，即f（x0）=0，利用单调性即可判断f（x1）的符号．
解答：函数
在（0．+∞）单调递减，f（x）=-lgx在（0．+∞）单调递减，
∴函数在（0．+∞）单调递减，
∵实数x0是函数y=f（x）的零点，
∴f（x0）=0，又∵0＜x1＜x0，
∴f（x1）＞f（x0）=0
故选A．
点评：此题是基础题．考查函数的零点与方程根的关系，以及根据函数解析式判断函数的单调性是解决此题的关键．
分析：根据函数
，利用指数函数和复合函数判断出它的单调性，根据实数x0是函数y=f（x）的零点，即f（x0）=0，利用单调性即可判断f（x1）的符号．解答：函数
在（0．+∞）单调递减，f（x）=-lgx在（0．+∞）单调递减，∴函数
在（0．+∞）单调递减，∵实数x0是函数y=f（x）的零点，
∴f（x0）=0，又∵0＜x1＜x0，
∴f（x1）＞f（x0）=0
故选A．
点评：此题是基础题．考查函数的零点与方程根的关系，以及根据函数解析式判断函数的单调性是解决此题的关键．
练习册系列答案
优加精卷系列答案
相关题目
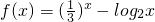，若实数x0是方程的解，且f（x）=0，0＜x1＜x0，则f（x1）的值为
，若实数x0是方程f（x）=0的解，且x1＞x0，则f（x1）的值
，若实数x0是方程f（x）=0的解，且0＜x1＜x0，则f（x1）的值
，若实数x0是函数y=f（x）的零点，且0＜x1＜x0，则f（x1）