题目内容
9．抛物线$y=-\frac{1}{8}{x^2}$的焦点坐标及准线方程分别为（ ）| A． | （0，-2），x=2 | B． | （0，-2），y=2 | C． | （2，0），x=-2 | D． | （2，0），y=-2 |
分析 求出抛物线的标准方程，利用x2=-2py（p＞0）的焦点坐标为（0，-$\frac{p}{2}$），准线方程为：y=$\frac{p}{2}$，求解判断即可．
解答 解：∵抛物线$y=-\frac{1}{8}{x^2}$化为：抛物线x2=-8y中，2p=8，解得p=4，
∴抛物线x2=-8y的焦点坐标为（0，-2），
准线方程为：y=2．
故选：B．
点评 本题考查抛物线的焦点坐标的求法，直线方程的求法，是基础题，解题时要认真审题，注意抛物线的简单性质的灵活运用．
练习册系列答案
相关题目
19．某运动员每次投篮的命中率为60%，现采用随机模拟的方法估计该运动员3次投篮恰好命中2次的概率，先由计算器产生0到9之间取整数值的随机表，指定1，2，3，4表示命不中，5，6，7，8，9，0表示命中，再以每3个随机数为一组，代表3次投篮的结果，经随机模拟产生了如下10组随机数：
907 966 191 925 271 932 812 458 569 683
据此估计，该运动员3次投篮恰好命中2次的概率为（ ）
907 966 191 925 271 932 812 458 569 683
据此估计，该运动员3次投篮恰好命中2次的概率为（ ）
| A． | 0.35 | B． | 0.30 | C． | 0.6 | D． | 0.70 |
20．函数y=sin（$\frac{5}{2}$π+2x）的图象的一条对称轴的方程是（ ）
| A． | $x=-\frac{π}{2}$ | B． | $x=-\frac{π}{4}$ | C． | $x=-\frac{π}{8}$ | D． | $x=\frac{5}{4}π$ |
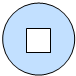欧阳修《卖油翁》中写到：“（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿”．可见“行行出状元”，卖油翁的技艺让人叹为观止，如右图铜钱是直径为4cm的圆形，正中间有边长为1cm的正方形孔，若随机向铜钱上滴一滴油（油滴是直径为0.2cm的球），记“油滴不出边界”为事件A，“油滴整体正好落入孔中”为事件B．则P（B|A）=$\frac{64}{361π}$（不作近似值计算）．
4．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，x∈R），则“f（x）在x=1处取最大值”是“f（x+1）为偶函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
1．已知i为虚数单位，复数z满足iz=3+4i，则|z|=（ ）
| A． | 25 | B． | 7 | C． | 5 | D． | 1 |