题目内容
如图,已知M是函数y=4-x2(0<x<2)图像C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A、B,O是坐标原点,求△AOB面积的最小值。

解:∵ ,∴y′=-2x,
,∴y′=-2x,
设 ,则过M点曲线C的切线斜率k=-2m,
,则过M点曲线C的切线斜率k=-2m,
∴切线方程为 ,
,
由x=0,得 ,
,
由y=0,得 ,其中0<m<2,
,其中0<m<2,
设△AOB的面积为S,则
 ,0<m<2,
,0<m<2,
∴ ,
,
令S′=0,得 ,解得
,解得 ,
,
当m∈ 时,S′<0,S在区间
时,S′<0,S在区间 上为减函数;
上为减函数;
当m∈ 时,S′>0,S在区间
时,S′>0,S在区间 上为增函数,
上为增函数,
∴当 时,S取得最小值,最小值为
时,S取得最小值,最小值为 。
。
 ,∴y′=-2x,
,∴y′=-2x,设
 ,则过M点曲线C的切线斜率k=-2m,
,则过M点曲线C的切线斜率k=-2m,∴切线方程为
 ,
,由x=0,得
 ,
,由y=0,得
 ,其中0<m<2,
,其中0<m<2,设△AOB的面积为S,则
 ,0<m<2,
,0<m<2,∴
 ,
,令S′=0,得
 ,解得
,解得 ,
,当m∈
 时,S′<0,S在区间
时,S′<0,S在区间 上为减函数;
上为减函数;当m∈
 时,S′>0,S在区间
时,S′>0,S在区间 上为增函数,
上为增函数,∴当
 时,S取得最小值,最小值为
时,S取得最小值,最小值为 。
。
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
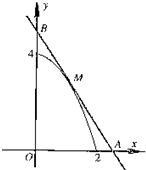 如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.
如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.

