题目内容
不等式组
的解集记为D，下列命题中正确的是（ ）
|
| A、?（x，y）∈D，x+2y≤3 |
| B、?（x，y）∈D，x+2y≥2 |
| C、?（x，y）∈D，x+2y≥-2 |
| D、?（x，y）∈D，x+2y≤-1 |
考点：全称命题,集合的表示法
专题：不等式的解法及应用,简易逻辑
分析：化简不等式组
，即可得出正确的结论．
|
解答：
解：∵不等式组
，
∴
，
∴
，
∴
，
∴x+2y≥0；
即x+2y≥-2．
∴若
的解集为D时，?（x，y）∈D，x+2y≥-2成立．
故选：C．
|
∴
|
∴
|
∴
|
∴x+2y≥0；
即x+2y≥-2．
∴若
|
故选：C．
点评：本题考查了不等式组的解法与应用问题，也考查了全称命题与特称命题的应用问题，是基础题目．
练习册系列答案
相关题目
若函数y=ax+b的部分图象如图所示，则（ ）
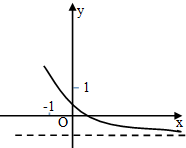
| A、0＜a＜1，-1＜b＜0 |
| B、0＜a＜1，0＜b＜1 |
| C、a＞1，-1＜b＜0 |
| D、a＞1，0＜b＜1 |
已知直线a，b，平面α，β，且a⊥α，b?β，则“a⊥b”是“α∥β”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合U={2，0，1，5}，集合A={0，2}，则∁UA=（ ）
| A、φ |
| B、{0，2} |
| C、{1，5} |
| D、{2，0，1，5} |
若U={1，2，3，4，5，6，}，M={1，2，5}，则∁UM=（ ）
| A、{2，4} |
| B、{1，3，6} |
| C、{3，5} |
| D、{3，4，6} |
设集合M={x|x=
，k∈Z}，N={x|x=
+
，k∈Z}，则M、N之间的关系为（ ）
| kπ |
| 2 |
| + |
. |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M?N | B、M?N |
| C、M=N | D、M∩N=∅ |