题目内容
已知数列{an},Sn是数列{an}的前n项和,且Sn=n2+n+1,则an=
.
|
|
分析:利用公式an=sn-sn-1,a1=s1 可求出数列{an}的通项an
解答:解:当n=1时,a1=s1=3
当n≥2时,an=sn-sn-1=n2+n+1-(n-1)2-(n-1)-1=2n
当n=1时,2n=2≠a1,
∴an=
故答案:an=
.
当n≥2时,an=sn-sn-1=n2+n+1-(n-1)2-(n-1)-1=2n
当n=1时,2n=2≠a1,
∴an=
|
故答案:an=
|
点评:本题考查数列的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
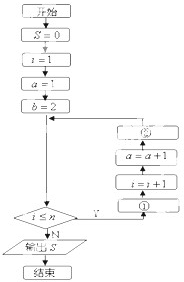 已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.
已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.