题目内容
已知△ABC中,2asinA=(2b+c)sinB+(2c+b)sinC,
(1)求角A的大小;
(2)求sinB+sinC的最大值,并指出此时角B的大小。
(1)求角A的大小;
(2)求sinB+sinC的最大值,并指出此时角B的大小。
解:(1)根据正弦定理得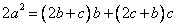 ,
,
所以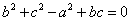 ,
,
所以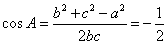 ,
,
又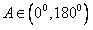 ,
,
所以∠A=120°。
(2)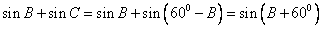 ,
,
所以,当∠B=30°时,sinB+sinC的最大值为1。
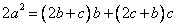 ,
,所以
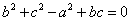 ,
,所以
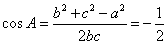 ,
,又
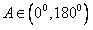 ,
,所以∠A=120°。
(2)
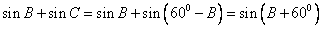 ,
,所以,当∠B=30°时,sinB+sinC的最大值为1。

练习册系列答案
相关题目