题目内容
17．焦点在x轴的椭圆，顺次连接椭圆的短轴顶点和焦点形成一边长为$\sqrt{2}$的正方形，求：（1）椭圆的标准方程；
（2）椭圆的焦点坐标、顶点坐标和离心率．
分析 （1）设椭圆的标准方程为：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），根据顺次连接椭圆的短轴顶点和焦点形成一边长为$\sqrt{2}$的正方形，可得b=c=1，a2=b2+c2．即可得出．
（2）由b=c=1，a2=2．即可得出椭圆的焦点坐标、顶点坐标和离心率．
解答 解：（1）设椭圆的标准方程为：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），∵顺次连接椭圆的短轴顶点和焦点形成一边长为$\sqrt{2}$的正方形，
∴b=c=1，∴a2=b2+c2=2．
∴椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1．
（2）由b=c=1，a2=2．
可得焦点坐标（±1，0），顶点$（±\sqrt{2}，0）$，（0，±1）．
离心率e=$\frac{c}{a}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$．
点评 本题考查了椭圆的标准方程及其性质、正方形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
9．命题“?x∈（-1，+∞），ln（x+1）＜x”的否定是（ ）
| A． | ?x∉（-1，+∞），ln（x+1）＜x | B． | ?x0∉（-1，+∞），ln（x0+1）＜x0 | ||
| C． | ?x∈（-1，+∞），ln（x+1）≥x | D． | ?x0∈（-1，+∞），ln（x0+1）≥x0 |
9．已知x，y满足约束条件$\left\{\begin{array}{l}{x-2y+4≥0}\\{x+y-2≤0}\\{y≥0}\\{\;}\end{array}\right.$，若目标函数z=ax-y仅在点（0，2）处取得最小值，则a的取值范围是（ ）
| A． | （-$\frac{1}{2}$，1） | B． | （-∞，-1）∪（$\frac{1}{2}$，+∞） | C． | （-1，$\frac{1}{2}$） | D． | （-∞，-$\frac{1}{2}$）∪（1，+∞） |
13．已知点（-$\sqrt{2}$，0）到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的距离为$\frac{\sqrt{5}}{5}$，则该双曲线的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{10}}{3}$ | D． | $\sqrt{5}$+1 |
6．将函数y=3sin（2x+$\frac{π}{3}$）图象上各点的横坐标伸长到原来的3倍，再向右平移$\frac{π}{8}$个单位，得到函数y=f（x）．则函数y=f（x）的解析式是（ ）
| A． | f（x）=3sin（$\frac{2x}{3}$+$\frac{π}{4}$） | B． | f（x）=3sin（$\frac{2x}{3}$$+\frac{5π}{24}$） | C． | f（x）=3sin（6x$-\frac{5π}{12}$） | D． | f（x）=3sin（6x$+\frac{5π}{24}$） |
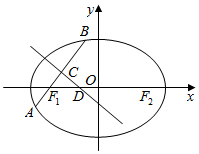如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{3}{2}$），且离心率为$\frac{1}{2}$．