Question

【题目】某同学用“五点法”画函数在某一个周期内的图像时，列表并填入了部分数据，如下表：

	0
	0	3	0		0

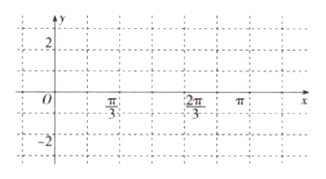
（1）请将上表数据补充完整，并写出函数的解析式（直接写出结果即可）；

（2）根据表格中的数据作出在一个周期内的图像；

（3）求函数在区间上的最大值和最小值.

Answer 1

【答案】（1）见解析，（2）见解析（3）；.

【解析】

（1）利用最大值求；由表格中数据先求周期,再求；再由求得,进而得到解析式,由解析式补全表格即可；

（2）由表格数据描点连线作图即可；

（3）令,则,利用正弦函数的性质求解即可

（1）根据题表中已知数据知,,所以,

因为,所以,所以,

则数据补全如下表：

	0
	0	3	0		0

（2）由（1）,在一个周期内的图像如图所示,

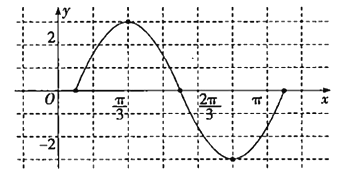
（3）令,则,

所以

在上的最值可转化为在上的最值,

因为正弦函数在区间上单调递减,在区间上单调递增,

所以在区间上单调递减,在区间上单调递增,

故的最小值为,最大值为,

当时,；当时,,

故当时,；当时,