题目内容

10．数列{an}满足a1=3，（an+1-2）（an+1）+2=0，则an=$\frac{{2}^{n}}{{2}^{n}-\frac{4}{3}}$．

分析 由（an+1-2）（an+1）+2=0，可得$\frac{{2}^{n+1}}{{a}_{n+1}}$-$\frac{{2}^{n}}{{a}_{n}}$=2n，利用叠加法，结合等比数列的求和公式可得结论．

解答 解：∵（an+1-2）（an+1）+2=0，
∴$\frac{{2}^{n+1}}{{a}_{n+1}}$-$\frac{{2}^{n}}{{a}_{n}}$=2n，
利用叠加法可得$\frac{{2}^{n}}{{a}_{n}}$=$\frac{2}{{a}_{1}}$+2+22+…+2n-1=$\frac{2}{3}$+$\frac{2（1-{2}^{n-1}）}{1-2}$=2n-$\frac{4}{3}$，
∴an=$\frac{{2}^{n}}{{2}^{n}-\frac{4}{3}}$．
故答案为：$\frac{{2}^{n}}{{2}^{n}-\frac{4}{3}}$．

点评 本题考查数列的通项，考查叠加法，等比数列的求和公式，正确变形是关键．

练习册系列答案
相关题目
20．已知函数f（x）=ax3+bx2+cx+d（a，b，c，d为实常数）在x=0处取得极小值2，且曲线y=f（x）在x=3处的切线方程为3x+y-11=0．
（1）求函数f（x）的解析式；
（2）已知函数h1（x）=ex+t[f′（x）+x2-x]，h2（x）=t[f′（x）+x2-x]-lnx．其中t为实常数，试探究是否存在区间M，使得h1（x）和h2（x）在区间M上具有相同的单调性，若存在，说明区间M应满足的条件及对应t的取值范围，并指出h1（x）和h2（x）在区间M上的单调性；若不存在．请说明理由．
1．设f（x）是定义在R上的奇函数，且当x≥0时，f（x）=x2，若对任意x∈[a，a+2]，不等式f（x+a）≥f（3x+1）恒成立，则实数a的取值范围是（-∞，-5]．
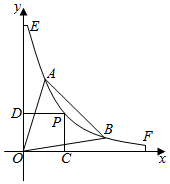18．家用电脑桌的桌面采用直线与弧线相结合，前部采用弧线，后部改用直线型．现将电脑桌靠在墙边，沿墙面建立如图所示的直角坐标系．弧线EF的方程为y=$\frac{60}{x}$（5≤x≤12）．键盘抽屉所在直线x+y-16=0与弧线交于A，B两点．拟在弧线EF上选取一点P分别作x轴、y轴的垂线．垂足为C，D．四边形OCPD（O为坐标原点）与三角形OAB的公共区域内放置电脑．设点P的坐标为（x，y）．公共部分面积为S．（单位：分米）
（1）求S关于x的表达式：
（2）求S的最大值及此时x的值．
5．已知（$\sqrt{x}$-$\frac{a}{x}$）6的展开式中含x${\;}^{\frac{3}{2}}$的项的系数为30，则实数a=-5．
15．已知复数z是方程x2+2x+10=0解，且Imz＜0，若$\frac{a}{z}$+$\overline{z}$=bi（其中a、b为实数，i为虚数单位，）Imz表示z的虚部）；
（I） 求复数w=a+bi的模；
（Ⅱ）若不等式x2+kx-a≥0在x∈[0，5]上恒成立，求实数k的取值范围．
2．若a、b表示两条直线，α表示平面，下列命题中的真命题为（　　）
A．若a⊥α，a⊥b，则b∥αB．若a∥α，a⊥b，则b⊥αC．若a⊥α，b⊆α，则a⊥bD．若a∥α，b∥α，则a∥b
19．已知直角△AOB的面积为1，O为直角顶点．设向量$\overrightarrow{a}$=$\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}$，$\overrightarrow{b}$=$\frac{\overrightarrow{OB}}{|\overrightarrow{OB}|}$，$\overrightarrow{OP}$=$\overrightarrow{a}$+2$\overrightarrow{b}$，则$\overrightarrow{PA}•\overrightarrow{PB}$的最大值为1．
20．已知集合A={-2，-1，0，1，2}，B={-1，0，1}，则映射f：A→B且f（x）为偶函数的种数共有（　　）
A．18B．21C．27D．36

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网