题目内容
(本题满分15分)如图,点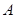 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心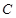 的定点,动点
的定点,动点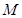 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点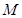 与点
与点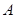 重合,设折痕
重合,设折痕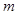 交线段
交线段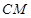 于点
于点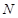 .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系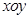 中,设圆
中,设圆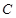 :
: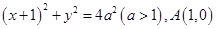 ,记点
,记点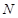 的轨迹为曲线
的轨迹为曲线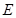 .
.
⑴证明曲线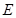 是椭圆,并写出当
是椭圆,并写出当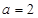 时该椭圆的标准方程;
时该椭圆的标准方程;
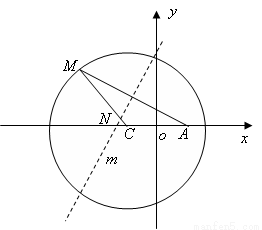
⑵设直线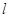 过点
过点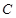 和椭圆
和椭圆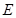 的上顶点
的上顶点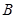 ,点
,点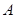 关于直线
关于直线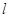 的对称点为点
的对称点为点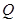 ,若椭圆
,若椭圆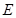 的离心率
的离心率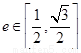 ,求点
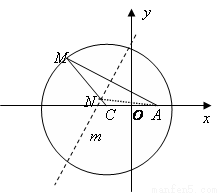
,求点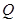 的纵坐标的取值范围.
的纵坐标的取值范围.
【答案】
(本题满分15分)
解:(1)连结NA, 由题意知,直线m是线段MA的中垂线,
∴NA=NM, 而圆C的半径为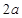 ……………………2分
……………………2分
∴NC+NA=NC+NM=CM=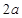 (常数)
(常数)
∴动点N到两定点C, A的距离之和为常数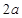 ,
,
所以,点N的轨迹是以定点C,
A为焦点,长轴长为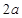 的椭圆
的椭圆
……………………4分
当 时,由于
时,由于 ,所以所求椭圆E的方程为
,所以所求椭圆E的方程为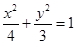
……………………6分
(2)椭圆E的方程为 ,其上顶点B
,其上顶点B
所以,直线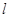 的方程为
的方程为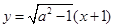 ,
……………………8分
,
……………………8分
记点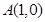 关于直线
关于直线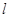 的对称点
的对称点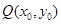
则有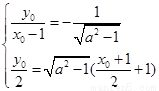 , 解得:
, 解得: ……………………11分;
……………………11分;
由 ,得
,得 ,
……………………12分
,
……………………12分
∴ ,令
,令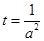 ,因为
,因为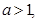 则
则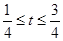 ,
,
∴ ,∴
,∴ ,
……………………14分
,
……………………14分
所以,点 的纵坐标的取值范围是
的纵坐标的取值范围是 ……………………15分
……………………15分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 中,底面
中,底面 是矩形,
是矩形, 平面
平面 与平面
与平面 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF. 的余弦值;
的余弦值;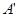 重合,求线段FM的长.
重合,求线段FM的长.
 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道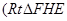 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
. 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
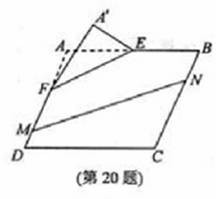 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别 上,
上, .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段