题目内容
(本题满分15分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, 与平面
与平面 所成角的正切值依次是
所成角的正切值依次是 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

(1)见解析;(2)直线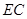 与平面
与平面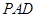 所成角的正弦值为
所成角的正弦值为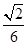 .
.
【解析】本试题主要是考查了面面垂直和线面角的求解的综合运用。
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。
解:(1)∵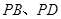 与平面
与平面 所成角的正切值依次
所成角的正切值依次
是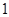 和
和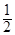 ,
,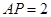 ∴
∴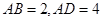
∵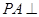 平面
平面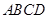 ,底面
,底面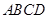 是矩形
是矩形
∴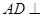 平面
平面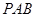 ∴
∴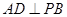
∵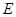 是
是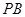 的中点 ∴
的中点 ∴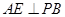
∴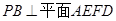 …………………………7分
…………………………7分
(2)解法一:∵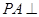 平面
平面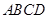 ,∴
,∴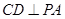 ,又
,又 ,
,
∴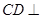 平面
平面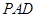 ,取
,取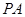 中点
中点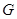 ,
,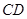 中点
中点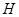 ,联结
,联结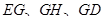 ,
,
则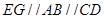 且
且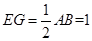 ,
,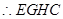 是平行四边形,
是平行四边形,
∴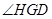 即为直线
即为直线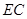 与平面
与平面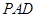 所成的角. 在
所成的角. 在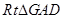 中,,
中,,  ,
,
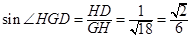 ,
,
∴直线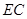 与平面
与平面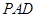 所成角的正弦值为
所成角的正弦值为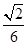 .
.
解法二:分别以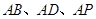 为
为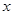 轴、
轴、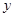 轴、
轴、 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,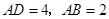 ,则各点坐标分别是
,则各点坐标分别是
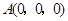 ,
,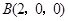 ,
,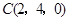 ,
,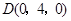 ,
,
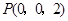 ,∴
,∴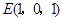 ,
,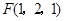 ,
,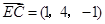 ,
,
又∵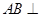 平面
平面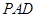 ,
,
∴平面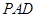 的法向量为
的法向量为 ,
,
设直线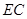 与平面
与平面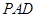 所成的角为
所成的角为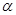 ,则
,则
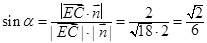 ,
,
∴直线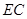 与平面
与平面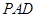 所成角的正弦值为
所成角的正弦值为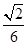 . …………………………15分
. …………………………15分
解:(1)∵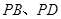 与平面
与平面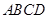 所成角的正切值依次
所成角的正切值依次
是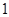 和
和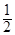 ,
,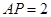 ∴
∴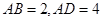
∵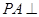 平面
平面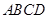 ,底面
,底面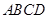 是矩形
是矩形
∴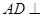 平面
平面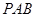 ∴
∴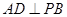
∵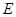 是
是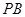 的中点 ∴
的中点 ∴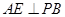
∴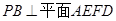 …………………………7分
…………………………7分
(2)解法一:∵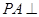 平面
平面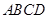 ,∴
,∴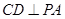 ,又
,又 ,
,
∴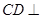 平面
平面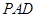 ,取
,取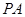 中点
中点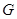 ,
,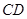 中点
中点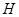 ,联结
,联结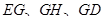 ,
,
则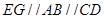 且
且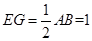 ,
,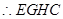 是平行四边形,
是平行四边形,
∴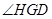 即为直线
即为直线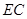 与平面
与平面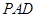 所成的角. 在
所成的角. 在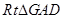 中,,
中,,  ,
,
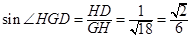 ,
,
∴直线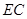 与平面
与平面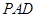 所成角的正弦值为
所成角的正弦值为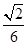 .
.
解法二:分别以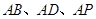 为
为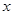 轴、
轴、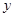 轴、
轴、 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,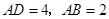 ,则各点坐标分别是
,则各点坐标分别是
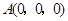 ,
,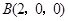 ,
,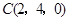 ,
,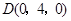 ,
,
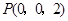 ,∴
,∴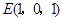 ,
,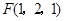 ,
,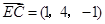 ,
,
又∵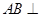 平面
平面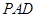 ,
,
∴平面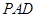 的法向量为
的法向量为 ,
,
设直线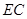 与平面
与平面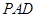 所成的角为
所成的角为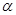 ,则
,则
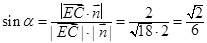 ,
,
∴直线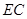 与平面
与平面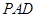 所成角的正弦值为
所成角的正弦值为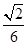 . …………………………15分
. …………………………15分

 快乐5加2金卷系列答案
快乐5加2金卷系列答案
 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF. 的余弦值;
的余弦值;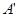 重合,求线段FM的长.
重合,求线段FM的长.
 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道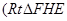 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
. 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
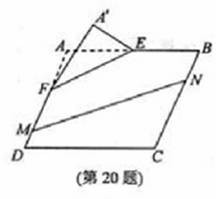 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别 上,
上, .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段