题目内容
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在整数
;(2)存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.
【解析】
试题分析:(1)由![]()
![]()
![]() ,设
,设![]() ,则
,则![]() ,利用导数工具求得
,利用导数工具求得![]() ,原命题可转化为
,原命题可转化为![]() 对
对![]() 恒成立
恒成立![]()
![]()
![]()
![]() 的取值范围为
的取值范围为![]() ;(2)易得
;(2)易得![]()
![]()
![]() ,利用分类讨论思想对
,利用分类讨论思想对![]() 、
、![]() 和
和![]() 分三种情况可得:存在整数
分三种情况可得:存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.
试题解析:(1)由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,
,
![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为![]() .
.
(2)![]() ,
,
∴![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 单调递增,无极值.
单调递增,无极值.
②当![]() 时,若
时,若![]() ,或
,或![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
∴当![]() 时,有极小值.
时,有极小值.
![]() 在
在![]() 上有极小值,∴
上有极小值,∴![]() .∴存在整数
.∴存在整数![]() .
.
③当![]() 时,若
时,若![]() 或
或![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() 有极小值.
有极小值.
![]() 在
在![]() 上有极小值,
上有极小值,
∴![]() ,得
,得![]() .
.
由①②③得,存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.

【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: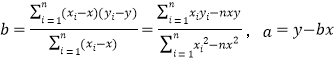 ,).
,).
【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()