题目内容
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
D
解析试题分析:因为 ,则由已知可得
,则由已知可得 时,
时, ,令
,令 ,则函数
,则函数 在
在 上单调递增。因为
上单调递增。因为 分别是在
分别是在 上的奇函数和偶函数,所以
上的奇函数和偶函数,所以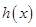 在
在 上是奇函数。则
上是奇函数。则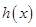 图像关于原点对称,且在
图像关于原点对称,且在 上也单调递增。因为
上也单调递增。因为 ,且
,且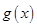 为偶函数则
为偶函数则 ,即
,即 。综上可得
。综上可得 的解集为
的解集为 。故D正确。
。故D正确。
考点:1函数的奇偶性;2用导数研究函数的单调性;3数形结合思想。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
设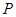 为曲线
为曲线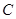 :
: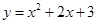 上的点,且曲线
上的点,且曲线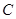 在点
在点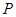 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为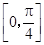 ,则点
,则点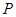 横坐标的取值范围为
横坐标的取值范围为
A.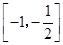 | B.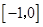 | C.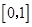 | D.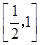 |
已知存在正数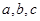 满足
满足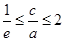 ,
,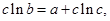 则
则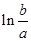 的取值范围是( )
的取值范围是( )
A.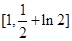 | B.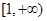 | C.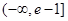 | D.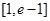 |
设函数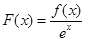 是定义在
是定义在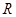 上的函数,其中
上的函数,其中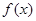 的导函数为
的导函数为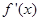 ,满足
,满足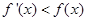 对于
对于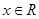 恒成立,则
恒成立,则
A.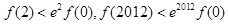 | B.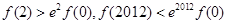 |
C.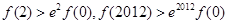 | D.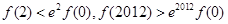 |
定义在R上的函数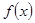 的图像如图所示,则关于
的图像如图所示,则关于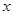 的不等式
的不等式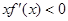 的解集为( )
的解集为( )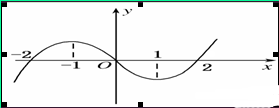
| A.(-2,-1)∪(1,2) | B.(-1,0)∪(1,+∞) |
| C.(-∞,-1)∪(0,1) | D.(-∞,-2)∪(2,+∞) |
曲线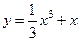 在点
在点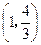 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A.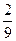 |
B.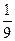 |
C.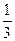 |
D.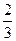 |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
| A.{x|x>0} | B.{x|x<0} |
| C.{x|x<-1或x>1} | D.{x|x<-1或0<x<1} |
 是
是 的导函数,
的导函数,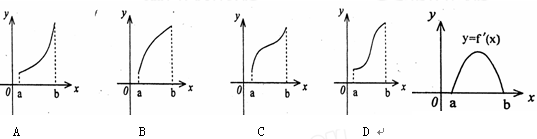
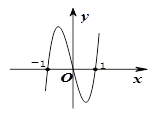
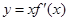 的图象如图所示(其中
的图象如图所示(其中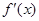 是函数
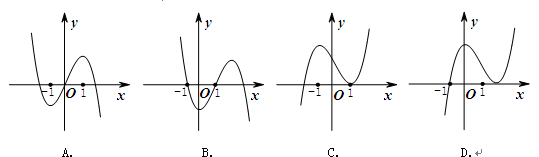
是函数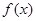 的导函数).下面四个图象中,
的导函数).下面四个图象中,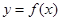 的图象大致是( )
的图象大致是( )