Question

已知△ABC的底边AB固定，长度为4，顶点C变动，且使tan∠CAB+tan∠CBA=4,求点C的轨迹方程.

 

Answer 1

解析：以底边AB的中点为原点，以AB边所在直线为x轴，建立如图所示的直角坐标系，

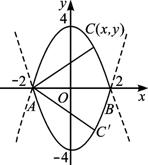
则A（-2，0）、B（2，0），设C(x,y).

当点C在x轴上方（y＞0）时，

∵tan∠CAB=k_CA=,tan∠CBA=-k_CB=-，

∴-=4.

∴y =-x²+4.

当点C在x轴下方（y＜0）时，

∵tan∠CAB=-k_CA=-,tan∠CBA=k_CB=,∴-+=4.

∴y=x²-4.

由此，点C的轨迹方程为y=-x²+4(y＞0)或y=x²-4(y＜0).