题目内容
已知△ABC的底边长为12,且底边BC固定,顶点A是动点,使sinB-sinC=解:建立适当的直角坐标系,令B(-6,0)、C(6,0)、A(x,y)为轨迹上任一点,则y≠0,|BC|=12.
因为sinB-sinC=![]() sinA,利用正弦定理,我们有|AC|-|AB|=
sinA,利用正弦定理,我们有|AC|-|AB|=![]() |BC|,结合双曲线定义,动点到两个定点C、B的距离之差为6,动点A位于以B、C为焦点的双曲线上.
|BC|,结合双曲线定义,动点到两个定点C、B的距离之差为6,动点A位于以B、C为焦点的双曲线上.
又注意到,此时A点只能在左支上,并且不能与左顶点重合.
双曲线中,∵2a=6,2c=12,∴a=3,c=6.∴b2=c2-a2=27.又∵中心在原点,两焦点在x轴上,
∴方程为![]() =1.∴点A的轨迹是双曲线
=1.∴点A的轨迹是双曲线![]() =1的左支,并且除去点(-3,0).
=1的左支,并且除去点(-3,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
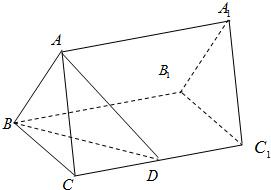 如图,已知正三棱柱ABC-A1B1C1的底边长是2,侧棱CC1的长是
如图,已知正三棱柱ABC-A1B1C1的底边长是2,侧棱CC1的长是 ,求点A的轨迹.
,求点A的轨迹.