Question

设双曲线的一个焦点为F；虚轴的一个端点为B，如果直线FB与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（　　）

• A．

  2

• B．

  5 -1

  2

• C．

  3 +1

  2

• D．

  5 +1

  2

Answer 1

分析：设该双曲线方程为

x2

a2

-

y2

b2

=1（a＞0，b＞0），得点B（0，b），焦点为F（c，0），直线FB的斜率为-

b

c

．由垂直直线的斜率之积等于-1，建立关于a、b、c的等式，变形整理为关于离心率e的方程，解之即可得到该双曲线的离心率．

解答：解：设该双曲线方程为

x2

a2

-

y2

b2

=1（a＞0，b＞0），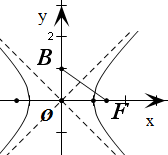
可得它的渐近线方程为y=±

b

a

x，焦点为F（c，0），
点B（0，b）是虚轴的一个端点
∴直线FB的斜率为k_FB=

0-b

c-0

=-

b

c

∵直线FB与直线y=

b

a

x互相垂直，
∴-

b

c

×

b

a

=-1，得b²=ac
∵b²=c²-a²，
∴c²-a²=ac，两边都除以a²，整理得e²-e-1=0
解此方程，得e=

1± 5

2

∵双曲线的离心率e＞1，∴e=

5 +1

2

（舍负）
故选：D

点评：本题给出双曲线的焦点与虚轴一端的连线与渐近线垂直，求它的离心率，着重考查了双曲线的标准方程与简单几何性质等知识，属于中档题．