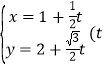题目内容
【题目】已知数列![]() 是首项为1的等差数列,数列
是首项为1的等差数列,数列![]() 是公比不为1的等比数列,且满足
是公比不为1的等比数列,且满足![]() ,
,![]() ,
,![]()
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)令![]() ,记数列
,记数列![]() 的前n项和为
的前n项和为![]() ,求证:对任意的
,求证:对任意的![]() ,都有
,都有![]() ;
;
(3)若数列![]() 满足
满足![]() ,
,![]() ,记
,记![]() ,是否存在整数
,是否存在整数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)存在整数
;(2)证明见解析;(3)存在整数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() 成立,理由见解析.
成立,理由见解析.
【解析】
(1)利用等差等比数列的基本量表示已知条件,解方程组得到基本量,利用等差等比数列的通项公式得到答案;
(2)根据(1)的结论得到数列![]() 的通项公式,利用指数的运算裂项,相消求和后得到
的通项公式,利用指数的运算裂项,相消求和后得到![]() 的表达式,判定单调性,然后利用不等式的基本性质即可证明;
的表达式,判定单调性,然后利用不等式的基本性质即可证明;
(3)假设存在满足要求的整数![]() ,取
,取![]() 得到
得到![]() 的范围,进而求得
的范围,进而求得![]() 的值为
的值为![]() ,然后证明当
,然后证明当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() 成立.为此先要根据
成立.为此先要根据![]() ,利用等比数列的求和公式,求得
,利用等比数列的求和公式,求得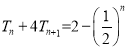 ,结合
,结合![]() ,求得
,求得![]() ,然后利用作差法证明即可.
,然后利用作差法证明即可.
(1)设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为
的公比为![]() ,
,
则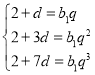 ,所以
,所以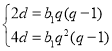 ,
,
因为![]() ,所以
,所以![]() .
.
所以 ,解得
,解得![]()
所以![]() ,
,![]() .
.
(2)因为![]()
![]()
![]()
所以![]()
![]()
![]()
![]()
![]()
又因为对任意的![]() ,都有
,都有![]() 单调递增,
单调递增,
即![]() ,
,
所以对任意的![]() ,都有
,都有![]() 成立;
成立;
(3)假设存在满足要求的整数![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ;
;
令![]() ,则
,则![]() ,解得
,解得![]() ;
;
令![]() ,则
,则![]() ,解得
,解得![]() ;
;
所以![]() ,
,
又已知![]() ,故若存在,则
,故若存在,则![]() .
.
下证:当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() 成立.
成立.
![]() ;
;
![]()
![]() ;
;
即![]()
![]()
![]()
又![]() ;
;
所以![]()
则![]()
![]()
![]()
![]()
![]()
![]()
而对任意的![]() ,
,![]() 单调递增,
单调递增,
所以![]()
即对任意的![]() 都有
都有![]() 成立,得证.
成立,得证.
所以,存在整数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() 成立.
成立.

【题目】某地区对当地的某种土特产的销售量y(吨)和销售单价x(元/千克)之间的关系进行了调查,得到下表中的数据:
销售单价x(元/千克) | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y(吨) | 5 | 6 | 8 | 10 | 11 | 14.1 |
(1)根据前5组数据,求出y关于x的回归直线方程.
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5,则认为回归直线方程是理想的,试问(1)中得到的回归直线方程是否理想?
(3)如果销售量y(吨)和销售单价x(元/千克)之间仍然服从(1)中的关系,进货成本为2.5元/千克,且货源充足(未售完的部分可按成本价全部售出),为了使利润最大,请你就如何确定销售单价给出合理建议.(每千克销售单价不超过12元)
参考公式:回归直线方程![]() ,其中
,其中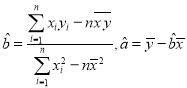 .
.
参考数据:![]() .
.