题目内容
如图,设 是一个高为
是一个高为 的四棱锥,底面
的四棱锥,底面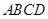 是边长为
是边长为 的正方形,顶点
的正方形,顶点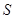 在底面上的射影是正方形
在底面上的射影是正方形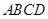 的中心.
的中心.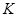 是棱
是棱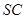 的中点.试求直线
的中点.试求直线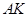 与平面
与平面 所成角的大小.
所成角的大小.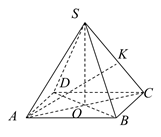
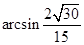
解析试题分析:本题是正四棱锥,这种特殊图形中,平行垂直的关系较多,解决问题的方法也很多,本来求直线与平面所成的角,应该作出直线在平面上的射影,求斜线与射影所来的锐角,根据这个我们也可以不作垂线,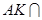 平面
平面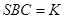 ,设点
,设点 到平面
到平面 的距离为
的距离为 ,则
,则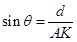 (
(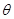 是
是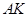 与平面
与平面 所成的角),
所成的角),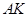 是
是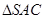 的中线,
的中线, 可看作三棱锥
可看作三棱锥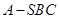 的高,可用体积法求得,问题易解。由于是正四棱锥,我们也可建立空间直角坐标系,用向量法求线面角.
的高,可用体积法求得,问题易解。由于是正四棱锥,我们也可建立空间直角坐标系,用向量法求线面角.
试题解析:法1:设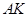 与平面
与平面 所成角为
所成角为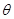 。因为
。因为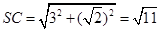 ,(2分)
,(2分)
所以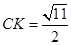 .所以
.所以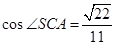 .(4分)
.(4分)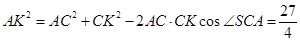 。所以
。所以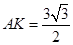 .(6分)
.(6分)
因为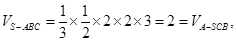 (8分)
(8分)
所以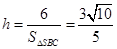 ,(10分)
,(10分)
因此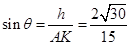 (11分)
(11分)
则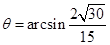 (12分)
(12分)
解法2: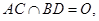 以
以 为坐标原点,
为坐标原点,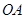 为
为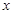 轴,
轴,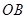 为
为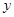 轴,
轴,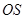 为
为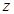 轴建立空间坐标系。则
轴建立空间坐标系。则 (4分)
(4分)
所以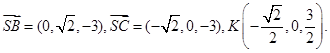 (6分)
(6分)
设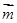 是平面
是平面 的一个法向量,易求得
的一个法向量,易求得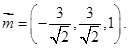 (8分)
(8分)
设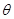 为
为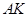 与平面
与平面 所成的角,因为
所成的角,因为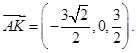 (10分)
(10分)
所以: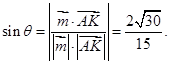 (11分)
(11分)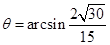 (12分)
(12分)
考点:直线与平面所成的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
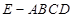 中,平面
中,平面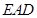
 平面
平面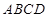 ,
,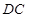 //
//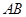 ,
,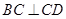 ,
,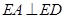 ,且
,且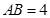 ,
,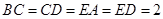 .
.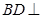 平面
平面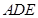 ;
;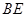 和平面
和平面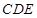 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点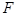 使得平面
使得平面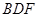
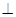 平面
平面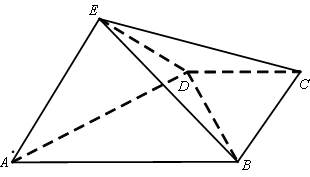
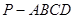 中,底面
中,底面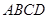 为矩形,
为矩形,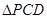 为等边三角形,
为等边三角形,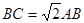 ,点
,点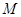 为
为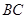 中点,平面
中点,平面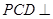 平面
平面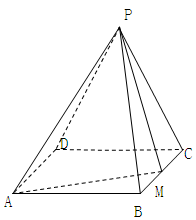
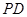 和
和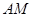 所成角的余弦值;
所成角的余弦值;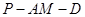 的大小.
的大小. AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.
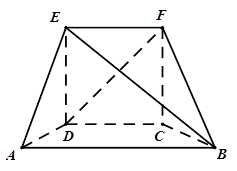
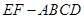 中,
中,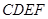 为边长为
为边长为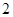 的正方形,
的正方形,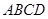 为直角梯形,
为直角梯形,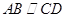 ,
,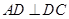 ,
,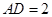 ,
,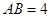 ,
,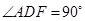 .
.
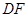 和
和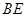 所成角的大小;
所成角的大小; 中,
中, 为
为 的中点,
的中点, ,
, ,
, .将此平面四边形
.将此平面四边形 折成直二面角
折成直二面角 ,
,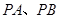 ,设
,设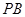 中点为
中点为 .
.
 平面
平面 ;
; 上是否存在一点
上是否存在一点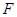 ,使得
,使得 平面
平面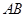 与平面
与平面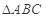 中,
中,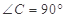 ,
, D、E分别是
D、E分别是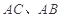 上的点,且
上的点,且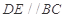 ,将
,将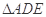 沿
沿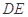 折起到
折起到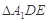 的位置,使
的位置,使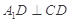 ,如图2.
,如图2.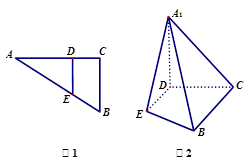
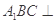 平面
平面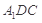 ;
;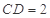 ,求
,求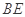 与平面
与平面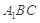 所成角的余弦值;
所成角的余弦值;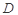 点在何处时,
点在何处时,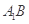 的长度最小,并求出最小值.
的长度最小,并求出最小值.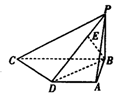
 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.