题目内容

3．已知向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-2，y），且$\overrightarrow a∥\overrightarrow b$，则|3$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{5}$．

分析 根据题意，由于$\overrightarrow a∥\overrightarrow b$可得1×y=（-2）×（-2），解可得y的值，即可得向量$\overrightarrow{b}$的坐标，由向量加法的坐标运算法则可得3$\overrightarrow{a}$+2$\overrightarrow{b}$的坐标，进而计算可得|3$\overrightarrow{a}$+2$\overrightarrow{b}$|，即可得答案．

解答 解：根据题意，向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-2，y），且$\overrightarrow a∥\overrightarrow b$，
则有1×y=（-2）×（-2），
解可得y=4，则向量$\overrightarrow{b}$=（-2，4）；
故3$\overrightarrow{a}$+2$\overrightarrow{b}$=（-1，2）；
则|3$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{（-1）^{2}+{2}^{2}}$=$\sqrt{5}$；
故答案为：$\sqrt{5}$．

点评 本题考查向量的坐标运算，关键是求出y的值，求出向量$\overrightarrow{b}$．

练习册系列答案
相关题目
14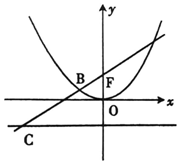．如图，过抛物线x2=2py（p＞0）的焦点F的直线l交抛物线于AB，交其准线于点C，若|BC|=2|BF|，且|AF|=2，则p=（　　）
A．1B．$\sqrt{2}$C．2D．2-$\sqrt{2}$
14．给出下列命题：
①若函数y=f（x）满足f（x-1）=f（x+1），则函数f（x）的图象关于直线x=1对称；
②点（2，1）关于直线x-y+1=0的对称点为（0，3）；
③通过回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$可以估计和观测变量的取值和变化趋势；
④正弦函数是奇函数，f（x）=sin（x2+1）是正弦函数，所以f（x）=sin（x2+1）是奇函数，上述推理错误的原因是大前提不正确．
其中真命题的序号是②③．
11．已知等差数列{an}的公差d不为0，且${a_{k_1}}$，${a_{k_2}}$，…，${a_{k_n}}$，…（k1＜k2＜…＜kn＜…）成等比数列，公比为q．
（1）若k1=1，k2=3，k3=8，求$\frac{a_1}{d}$的值；
（2）当$\frac{a_1}{d}$为何值时，数列{kn}为等比数列；
（3）若数列{kn}为等比数列，且对于任意n∈N*，不等式${a_n}+{a_{k_n}}＞2{k_n}$恒成立，求a1的取值范围．
18．若1≤log2（x-y+1）≤2，|x-3|≤1，则x-2y的最大值与最小值之和是（　　）
A．0B．-2C．2D．6
8．已知集合A={x|x2+x-6＜0}，B={x|3x＞1}，则A∩（∁RB）=（　　）
A．（-3，1]B．（1，2）C．（-3，0]D．[1，2）
15．在△ABC中，角A，B，C的对边分别为a，b，c
（1）若a，b，c成等比数列，$cosB=\frac{12}{13}$，求$\frac{cosA}{sinA}+\frac{cosC}{sinC}$的值；
（2）若A，B，C成等差数列，且b=2，设A=α，△ABC的周长为l，求l=f（α）的最大值．
12．已知f（x）=|x+1|+|x-1|．
（Ⅰ）求不等式f（x）＜4的解集；
（Ⅱ）若不等式f（x）-|a-1|＜0有解，求a的取值范围．
13．已知$\overrightarrow a=（sinx，cosx），\overrightarrow b=（sinx，sinx），f（x）=2\overrightarrow a•\overrightarrow b$．
（Ⅰ）求f（x）的最小正周期和最大值；
（Ⅱ）画出函数y=f（x）在区间$[{-\frac{π}{2}，\frac{π}{2}}]$上的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网