题目内容
【题目】已知斜率为1的直线
与椭圆
交于
，
两点，且线段
的中点为
，椭圆
的上顶点为
.
（1）求椭圆的离心率；
（2）设直线
与椭圆交于
两点，若直线
与
的斜率之和为2，证明：
过定点.
【答案】（1）
（2）见证明
【解析】
（1）设点P，Q的坐标，代入椭圆C的方程，利用点差法及中点坐标公式可得a，b的关系，可得e；
（2）联立直线
方程与椭圆方程，利用根与系数的关系可得M，N的横坐标的和与积，由直线AM与AN的斜率之和为2可得m与k的关系，再由直线系方程得答案．
（1）设点
，
，由于点
为线段
的中点
所以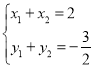
，
又
两式作差
，
所以
，即；
（2）由（1）结合上顶点
，椭圆的方程为
，
设点
，
联立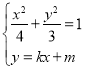
得
，则韦达定理得，
据题意可得
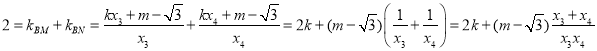代入韦达定理得
，化简得
，
所以直线为
，过定点
，
综上，直线过定点.
练习册系列答案
阅读快车系列答案
相关题目
