题目内容

A={x|x2+x-6=0}，B={x|mx+1=0}且A∪B=A，则m的取值范围（　　）
A．{
1
3
，-
1
2
}		B．{0，-
1
3
，-
1
2
}		C．{0，
1
3
，-
1
2
}		D．{
1
3
，
1
2
}
∵A={x|x2+x-6=0}={-3，2}，
A∪B=A，则B⊆A
若m=0，则B=∅，满足要求；
若m≠0，则B={x|x=-
1
m
}
则m=
1
3
，或m=-
1
2

综上m的取值范围组成的集合为{0，
1
3
，-
1
2
}
故选C
练习册系列答案
相关题目
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
已知全集U=R，集合A={x|x2-x＞0}，则?UA等于（　　）
已知集合A={x|-x2+x+2＞0}，B={x|-1＜x＜1}，则A∩（?UB）=（　　）
（2007广州市水平测试）已知集合A={x|x2-x＜0}，B={x|-2＜x＜2}，则A∩B=（　　）
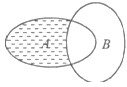精英家教网已知全集U=R，集合A={x|x2+x-2＜0}，B={x|0＜x＜3}，则图中阴影部分所表示的集合为（　　）
A、{x|-2＜x≤0}B、{x|0＜x＜1}C、{x|1≤x＜3}D、{x|x≤-2或x≥3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网