Question

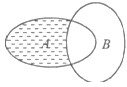已知全集U=R，集合A={x|x²+x-2＜0}，B={x|0＜x＜3}，则图中阴影部分所表示的集合为（　　）

• A、{x|-2＜x≤0}
• B、{x|0＜x＜1}
• C、{x|1≤x＜3}
• D、{x|x≤-2或x≥3}

Answer 1

分析：根据图象确定阴影部分对应的集合，然后根据集合的基本运算即可得到结论．

解答：解：由图中可知，阴影部分对应的集合为A∩∁_UB，
∵A={x|x²+x-2＜0}={x|-2＜x＜0}，B={x|0＜x＜3}，
∴∁_UB={x|x≥3或x≤0}，
即A∩∁_UB={x|-2＜x≤0}，
故选：A．

点评：本题主要考查集合的基本运算，利用Venn图确定阴影部分的集合是解决本题的关键，比较基础．