题目内容
【题目】如图,过抛物线![]() 上一点
上一点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,当
,当![]() 与
与![]() 的斜率存在且倾斜角互补时:
的斜率存在且倾斜角互补时:

(1)求![]() 的值;
的值;
(2)若直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 时,求
时,求![]() 面积
面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由抛物线![]() 过点
过点![]() ,得
,得![]() .由
.由![]() ,
,![]() 倾斜角互补可知
倾斜角互补可知![]() ,即
,即![]() ,由
,由![]() ,代入得
,代入得![]() ;(2)利用点差法求得
;(2)利用点差法求得![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线的方程和抛物线的方程利用弦长公式和点到直线距离公式计算面积
,联立直线的方程和抛物线的方程利用弦长公式和点到直线距离公式计算面积![]() ,利用导数求得面积的最大值为
,利用导数求得面积的最大值为![]() .
.
试题解析:
(1)由抛物线![]() 过点
过点![]() ,得
,得![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
由![]() ,
,![]() 倾斜角互补可知
倾斜角互补可知![]() ,即
,即![]() ,
,
由![]() ,代入得
,代入得![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,由
,由![]() ,得
,得![]() ,
,
由(1)得![]() ,将其代入上式得
,将其代入上式得![]() .
.
因此设直线![]() 的方程为
的方程为![]() ,由
,由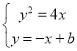 ,消去
,消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,这时
,这时![]() ,
,
![]() ,又点
,又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
令![]() ,则由
,则由![]() ,得
,得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,所以
,所以![]() 单调递减,
单调递减,
故![]() 的最大值为
的最大值为![]() ,故
,故![]() 面积
面积![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目