题目内容
在△ABC中,2B=A+C,a+
b=2c,求sinC.
| 2 |
考点:余弦定理
专题:解三角形
分析:△ABC中,由条件求得 B=
,A+C=
.由a+
b=2c,利用正弦定理化简求得cosA=
,可得A=
,从而求得C=
-A的值,从而求得sinC的值.
| π |
| 3 |
| 2π |
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 2π |
| 3 |
解答:
解:△ABC中,∵2B=A+C,∴B=
,A+C=
.
∵a+
b=2c,故由正弦定理可得sinA=2sinC-
sinB=2sin(
-A)-
•
,
即sinA=2×
cosA-2×(-
)sinA-
,求得cosA=
,∴A=
,∴C=
-A=
,
∴sinC=sin(
+
)=sin
cos
+cos
sin
=
.
| π |
| 3 |
| 2π |
| 3 |
∵a+
| 2 |
| 2 |
| 2π |
| 3 |
| 2 |
| ||
| 2 |
即sinA=2×
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| 5π |
| 12 |
∴sinC=sin(
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| ||||
| 4 |
点评:本题主要考查正弦定理、三角函数的恒等变换及化简求值,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
下列椭圆的形状哪一个更圆( )
| A、9x2+y2=36 | ||||
B、
| ||||
| C、x2+9y2=36 | ||||
D、
|
圆心角为1rad,半径为1的扇形的面积为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、π |
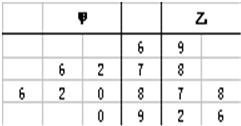 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分比乙同学平均分高;
③甲同学成绩的平均分比乙同学平均分低;
④甲同学成绩的方差小于乙同学成绩的方差.
| A、①③ | B、①②④ | C、③④ | D、③ |
给出以下命题:
(1)若
f(x)dx>0,则f(x)>0;
(2)
dx=0;
(3)应用微积分基本定理,有
dx=F(2)-F(1),则F(x)=lnx;
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
f(x)dx=
f(x)dx;
其中正确命题的为( )
(1)若
| ∫ | b a |
(2)
| ∫ | 2π -2π |
| sinx |
| e|x| |
(3)应用微积分基本定理,有
| ∫ | 2 1 |
| 1 |
| x |
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
| ∫ | a 0 |
| ∫ | a+T T |
其中正确命题的为( )
| A、(3),(4) |
| B、(1),(2) |
| C、(1),(4) |
| D、(2),(4) |