题目内容
设F为双曲线
-
=1的左焦点,在x轴上F点的右侧有一点A,以FA为直径的圆与双曲线左、右两支在x轴上方的交点分别为M,N,则
的值为( )
| x2 |
| 16 |
| y2 |
| 9 |
| |FN|-|FM| |
| |FA| |
分析:对点A特殊化,不妨设点A为双曲线的右焦点,依题意得F(-5,0),A(5,0),|FN|-|NA|=8,|FM|=|NA|,所以|FN|-|FM|=8,从而能够得到结果.
解答:解:由于F为双曲线
-
=1的左焦点,在x轴上F点的右侧有一点A,
以FA为直径的圆与双曲线左、右两支在x轴上方的交点分别为M,N,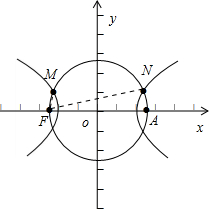
不妨设A为椭圆的右焦点,则F(-5,0),A(5,0),|FN|-|NA|=8,
由双曲线的对称性得到|FM|=|NA|,
∴|FN|-|FM|=8
则
=
=
.
故选:D.
| x2 |
| 16 |
| y2 |
| 9 |
以FA为直径的圆与双曲线左、右两支在x轴上方的交点分别为M,N,

不妨设A为椭圆的右焦点,则F(-5,0),A(5,0),|FN|-|NA|=8,
由双曲线的对称性得到|FM|=|NA|,
∴|FN|-|FM|=8
则
| |FN|-|FM| |
| |FA| |
| 8 |
| 10 |
| 4 |
| 5 |
故选:D.
点评:本题考查圆锥曲线的性质和应用,解题时要注意合理地选取特殊点.

练习册系列答案
相关题目
设A为双曲线
-
=1右支上一点,F为该双曲线的右焦点,连AF交双曲线于B,过B作直线BC垂直于双曲线的右准线,垂足为C,则直线AC必过定点( )
| x2 |
| 16 |
| y2 |
| 9 |
A、(
| ||
B、(
| ||
| C、(4,0) | ||
D、(
|