题目内容
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足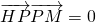 ,
,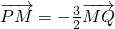 .
.
①当点P在y轴上移动时,求点M的轨迹C;
②过点R(2,1)作直线l与轨迹C交于A,B两点,使得R恰好为弦AB的中点,求直线l的方程.
解:①设点M(x,y),由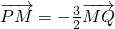 ,得
,得 ,
, ,
,
由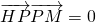 ,得
,得 ,所以y2=4x.
,所以y2=4x.
又点Q在x轴的正半轴上,得x>0.
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点.
②方法一:设直线l:y=k(x-2)+1,其中k≠0,代入y2=4x,
整理得k2x2-(4k2-2k+4)x+(2k-1)2=0,
设A(x1,y1),B(x2,y2),
则 ,
,
由 ,解得:k=2.
,解得:k=2.
所以,直线l的方程为y=2(x-2)+1,
即:y=2x-3.
方法二:设A(x1,y1),B(x2,y2),
则 ,
, ,
,
两式相减 得: .
.
整理得: ,
,
因为R(2,1)为弦AB的中点,
所以y1+y2=2,
代入上式得 ,即kAB=2.
,即kAB=2.
所以,直线l的方程为y=2(x-2)+1,
即:y=2x-3
分析:①设点M(x,y),由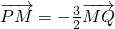 ,得
,得 ,
, ,由
,由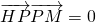 ,得
,得 ,所以y2=4x.由此能求出点M的轨迹C.
,所以y2=4x.由此能求出点M的轨迹C.
②方法一:
设直线l:y=k(x-2)+1,其中k≠0,代入y2=4x,整理得k2x2-(4k2-2k+4)x+(2k-1)2=0.设A(x1,y1),B(x2,y2),则 ,由
,由 ,解得:k=2.由此能求出直线l的方程为.
,解得:k=2.由此能求出直线l的方程为.
方法二:
设A(x1,y1),B(x2,y2),则 ,
, ,两式相减 得:
,两式相减 得: .因为R(2,1)为弦AB的中点,所以y1+y2=2,由此能求出直线l的方程.
.因为R(2,1)为弦AB的中点,所以y1+y2=2,由此能求出直线l的方程.
点评:本题考查直线与圆锥曲线的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
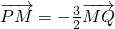 ,得
,得 ,
, ,
,由
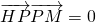 ,得
,得 ,所以y2=4x.
,所以y2=4x.又点Q在x轴的正半轴上,得x>0.
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点.
②方法一:设直线l:y=k(x-2)+1,其中k≠0,代入y2=4x,
整理得k2x2-(4k2-2k+4)x+(2k-1)2=0,
设A(x1,y1),B(x2,y2),
则
 ,
,由
 ,解得:k=2.
,解得:k=2.所以,直线l的方程为y=2(x-2)+1,
即:y=2x-3.
方法二:设A(x1,y1),B(x2,y2),
则
 ,
, ,
,两式相减 得:
 .
.整理得:
 ,
,因为R(2,1)为弦AB的中点,
所以y1+y2=2,
代入上式得
 ,即kAB=2.
,即kAB=2.所以,直线l的方程为y=2(x-2)+1,
即:y=2x-3
分析:①设点M(x,y),由
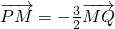 ,得
,得 ,
, ,由
,由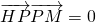 ,得
,得 ,所以y2=4x.由此能求出点M的轨迹C.
,所以y2=4x.由此能求出点M的轨迹C.②方法一:
设直线l:y=k(x-2)+1,其中k≠0,代入y2=4x,整理得k2x2-(4k2-2k+4)x+(2k-1)2=0.设A(x1,y1),B(x2,y2),则
 ,由
,由 ,解得:k=2.由此能求出直线l的方程为.
,解得:k=2.由此能求出直线l的方程为.方法二:
设A(x1,y1),B(x2,y2),则
 ,
, ,两式相减 得:
,两式相减 得: .因为R(2,1)为弦AB的中点,所以y1+y2=2,由此能求出直线l的方程.
.因为R(2,1)为弦AB的中点,所以y1+y2=2,由此能求出直线l的方程.点评:本题考查直线与圆锥曲线的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足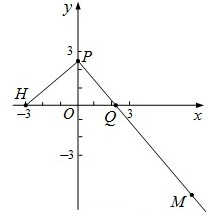 (2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足
(2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足