题目内容
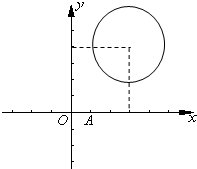
若x,y满足x2+y2-2x+4y=0,则x-2y的最大值为( )
| A.0 | B.5 | C.-10 | D.10 |
先根据x,y满足x2+y2-2x+4y=0,可得点(x,y)在以(1,-2)为圆心,
以
为半径的圆上,画出图形.
设z=x-2y,则 y=
-
,将-
作为直线z=x-2y在y轴上的截距,故当-
最小时,z最大.
当直线z=x-2y经过直线OC和圆的交点A(2,-4)时,直线在y轴上的截距-
最小,z最大.
把点A(2,-4)代入z=x-2y可得z的最大值为:10. 故x-2y的最大值为10.
故选:D.

以
| 5 |
设z=x-2y,则 y=
| x |
| 2 |
| z |
| 2 |
| z |
| 2 |
| z |
| 2 |
当直线z=x-2y经过直线OC和圆的交点A(2,-4)时,直线在y轴上的截距-
| z |
| 2 |
把点A(2,-4)代入z=x-2y可得z的最大值为:10. 故x-2y的最大值为10.
故选:D.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
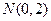 ,且与定直线
,且与定直线 相切.
相切.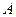 、
、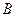 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且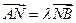 . 分别以
. 分别以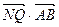 为定值.
为定值.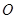 引圆
引圆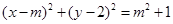 的切线
的切线 ,当
,当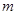 变化时,切点
变化时,切点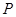 的轨迹方程是( )
的轨迹方程是( )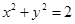

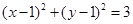
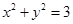
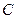 和
和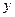 轴相切,圆心在直线
轴相切,圆心在直线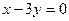 上,且被直线
上,且被直线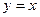 截得的弦长为
截得的弦长为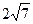
 ,求圆
,求圆