题目内容
设椭圆M：
(a＞b＞0)的离心率为
，长轴长为6
，设过右焦点F，
（Ⅰ）求椭圆M的方程；
（Ⅱ）设过右焦点F倾斜角为θ的直线交椭M于A，B两点，求证|AB|=
。
(a＞b＞0)的离心率为，长轴长为6，设过右焦点F，（Ⅰ）求椭圆M的方程；
（Ⅱ）设过右焦点F倾斜角为θ的直线交椭M于A，B两点，求证|AB|=
。 解：（Ⅰ）
，
所求椭圆M的方程为
；
（Ⅱ）当θ≠
，设直线AB的斜率为k=tanθ，焦点F(3，0)，
则直线AB的方程为y=k(x-3) ，
有
(1+2k2)x2-12k2x+18(k2-1)=0，
设点A(x1，y1)，B(x2，y2) ，
有x1+x2=
，x1x2=
，
|AB|=
，**
又因为k=tanθ=
代入**式得
|AB|=
；
当θ=
时，直线AB的方程为x=3，此时|AB|=
；
而当θ=
时，|AB|=
=
；
综上所述，所以|AB|=
。
，所求椭圆M的方程为
；（Ⅱ）当θ≠
，设直线AB的斜率为k=tanθ，焦点F(3，0)，则直线AB的方程为y=k(x-3) ，
有
(1+2k2)x2-12k2x+18(k2-1)=0，设点A(x1，y1)，B(x2，y2) ，
有x1+x2=
，x1x2=，|AB|=
，**又因为k=tanθ=
代入**式得|AB|=
；当θ=
时，直线AB的方程为x=3，此时|AB|=；而当θ=
时，|AB|==；综上所述，所以|AB|=
。
练习册系列答案
相关题目
(a＞b＞0)的离心率为
，长轴长为
，设过右焦点F。
的直线交椭M于A，B两点，求证| AB | =
。
(a＞b＞0)的离心率为
，长轴长为
，设过右焦点F倾斜角为
的直线交椭圆M于A，B两点。
；
(a＞b＞0)的离心率与双曲线
的离心率互为倒数，且内切于圆
．
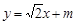交椭圆于A、B两点，椭圆上一点
，
(a＞b＞0)的离心率为
，长轴长为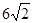
，设过右焦点F倾斜角为
的直线交椭圆M于A，B两点。
(a＞b＞0)的离心率为
，长轴长为
，设过右焦点F倾
的直线交椭圆M于A，B两点。