题目内容
设有两组实数a1、a2、b1、b2,那么有(a1b1+a2b2)2≤(a12+a22)(b12+b22),当且仅当a1∶b1=a2∶b2时等号成立.
证明:∵在直角坐标平面上,设![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),∠AOB=θ,
=(b1,b2),∠AOB=θ,
∴|![]() |=
|=![]() ,
,
|![]() |=
|=![]() ,
,
![]() ·
·![]() =|
=|![]() ||
||![]() |cosθ
|cosθ
=![]() ·
·![]() cosθ.
cosθ.
又![]() ·
·![]() =a1b1+a2b2,
=a1b1+a2b2,
∴cosθ= .
.
而|cosθ|≤1,
∴(a1b1+a2b2)2≤(a12+a22)(b12+b22).
∴当cosθ=±1![]()
![]() ∥
∥![]() (
(![]() ≠0)
≠0)![]() a1∶b1=a2∶b2时,等号成立.
a1∶b1=a2∶b2时,等号成立.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
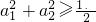 证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即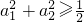 根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为:________.
根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为:________.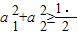 证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即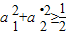 根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为: .
根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为: .