题目内容
请阅读下列材料:若两个实数a1,a2满足a1+a2=1,则
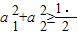 证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即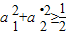 根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为: .
根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为: .
【答案】分析:由题意,a1+a2=1,两数的平方和大于等于 ,则n个数的和为1时,应该类比为n个数的平方和大于等于
,则n个数的和为1时,应该类比为n个数的平方和大于等于
解答:解:由题意若两个实数a1,a2满足a1+a2=1,则
∴若n个实数a1,a2,…,an满足a1+a2+…+an=1时,有
故答案为:
点评:本题考查类比推理,由类比推理得出的结论不一定正确求解本题的关键是找出类比的标准及类比的方式来.如本题,和为1是一个共性, 对
对 .
.
 ,则n个数的和为1时,应该类比为n个数的平方和大于等于
,则n个数的和为1时,应该类比为n个数的平方和大于等于
解答:解:由题意若两个实数a1,a2满足a1+a2=1,则

∴若n个实数a1,a2,…,an满足a1+a2+…+an=1时,有

故答案为:

点评:本题考查类比推理,由类比推理得出的结论不一定正确求解本题的关键是找出类比的标准及类比的方式来.如本题,和为1是一个共性,
 对
对 .
. 
练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
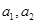 满足
满足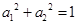 ,那么
,那么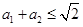 .证明:构造函数
.证明:构造函数 ,因为对一切实数
,因为对一切实数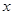 ,恒有
,恒有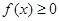 ,所以
,所以 ,从而得
,从而得 ,所以
,所以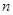 个正实数满足
个正实数满足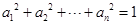 时,你能得到的结论为 .(不必证明)
时,你能得到的结论为 .(不必证明)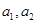 满足
满足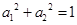 ,那么
,那么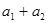 ≤
≤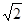 .
.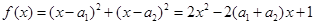 ,因为对一切实数
,因为对一切实数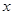 ,恒有
,恒有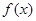 ≥0,所以△≤0,从而得
≥0,所以△≤0,从而得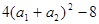 ≤0,所以
≤0,所以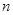 个正实数满足
个正实数满足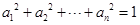 时,你能得到的结论为 ▲ .
时,你能得到的结论为 ▲ . 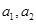 满足
满足 ,那么
,那么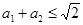 。证明:构造函数
。证明:构造函数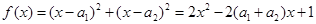 ,因为对一切实数x,恒有
,因为对一切实数x,恒有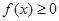 ,所以
,所以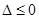 ,从而得
,从而得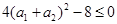 ,所以
,所以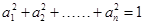 时,你能得到的结论为
。
时,你能得到的结论为
。