题目内容
如图所示,正方体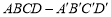 的棱长为1,
的棱长为1, 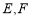 分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱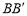 、
、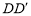 交于
交于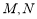 ,设
,设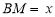 ,
, ,给出以下四个命题:
,给出以下四个命题:

(1)平面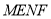
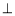 平面
平面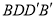 ;
;
(2)当且仅当x=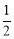 时,四边形
时,四边形 的面积最小;
的面积最小;
(3)四边形 周长
周长 ,
, 是单调函数;
是单调函数;
(4)四棱锥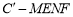 的体积
的体积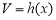 为常函数;
为常函数;
以上命题中假命题的序号为( )
A.(1)(4) B.(2) C.(3) D.(3)(4)
C
【解析】
试题分析:(1)由于 ,
, ,则
,则 ,则
,则 ,又因为
,又因为 ,则平面
,则平面
 平面
平面 ;(2)由于四边形
;(2)由于四边形 为菱形,
为菱形, ,
, ,要使四边形
,要使四边形 的面积最小,只需
的面积最小,只需 最小,则当且仅当
最小,则当且仅当 时,四边形
时,四边形 的面积最小;(3)因为
的面积最小;(3)因为 ,
, ,
, 在
在 上不是单调函数;(4)
上不是单调函数;(4) ,
, =
= ,
, 到平面
到平面 的距离为1,
的距离为1, ,又
,又 ,
, ,
, 为常函数.
为常函数.
故选(3)
考点:1.面面垂直的判定定理;2.建立函数模型.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
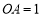 ,在以
,在以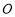 为圆心,以
为圆心,以 为半径的半圆弧上随机取一点B,则
为半径的半圆弧上随机取一点B,则 的面积小于
的面积小于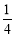 的概率为 .
的概率为 .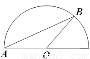
 ;
;
 ⊥平面
⊥平面 ,
,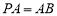 ,
,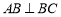 ,
,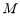 为
为 中点.
中点.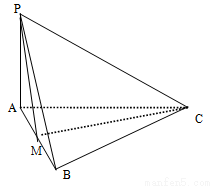
 ;
;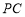 与平面
与平面 所成角的正切值 为
所成角的正切值 为 ,求二面角
,求二面角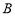 -
- -
- 的正弦值.
的正弦值. 的直线
的直线 与圆
与圆 交于A,B两点,C为圆心,当
交于A,B两点,C为圆心,当 最小时,直线
最小时,直线 中,点
中,点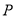 在线段
在线段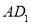 上运动,则异面直线
上运动,则异面直线 与
与 所成的角
所成的角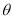 的取值范围是( )
的取值范围是( )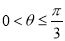 B.
B.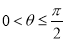 C.
C. D.
D.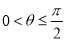
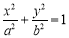 (a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为
(a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为 -1.过F作椭圆的弦PQ,直线AP,AQ分别交直线
-1.过F作椭圆的弦PQ,直线AP,AQ分别交直线 于点M,N.
于点M,N.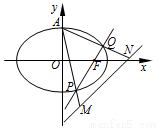
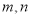 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列命题,正确的是( )
是三个不同的平面,给出下列命题,正确的是( )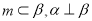 ,则
,则
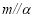 ,
, ,则
,则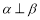
 ,
, ,则
,则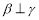
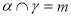 ,
, ,
,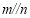 ,则
,则 [
[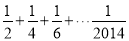 的值的程序框图,其中判断框内应填入的是( ).
的值的程序框图,其中判断框内应填入的是( ).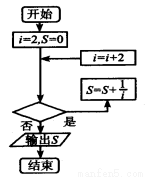
 B.
B.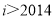 C.
C.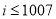 D.
D.