题目内容
(本小题10分). 如图,设椭圆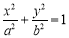 (a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为
(a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为 -1.过F作椭圆的弦PQ,直线AP,AQ分别交直线
-1.过F作椭圆的弦PQ,直线AP,AQ分别交直线 于点M,N.
于点M,N.
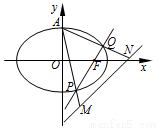
(Ⅰ) 求椭圆的方程;
(Ⅱ) 求当三角形AMN面积最小时直线PQ的方程.
(1)
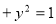 .(2)
.(2)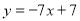
【解析】
试题分析:首先利用题目所给的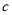 和
和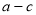 求出
求出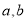 得到椭圆方程,第二步先设出过焦点
得到椭圆方程,第二步先设出过焦点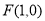 的直线
的直线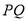 的方程
的方程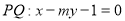 ,与椭圆方程联立方程组,消去
,与椭圆方程联立方程组,消去 后得到关于
后得到关于 的元二次方程,设
的元二次方程,设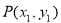 ,
,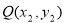 ,根据根与系数关系得出
,根据根与系数关系得出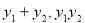 ,再利用两点式写出直线
,再利用两点式写出直线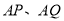 的方程与直线
的方程与直线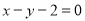 联立,求出
联立,求出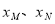 ,求出
,求出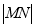 的表达式,最后借助换元法求
的表达式,最后借助换元法求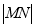 最小值,由于点
最小值,由于点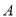 到直线
到直线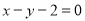 的距离为定值,三角形AMN面积最小只需
的距离为定值,三角形AMN面积最小只需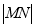 最小,最后再求出直线PQ的方程.
最小,最后再求出直线PQ的方程.
试题解析:(Ⅰ) 由题意知,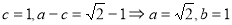 ,所以椭圆方程为
,所以椭圆方程为 
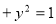 .
.
(Ⅱ) 设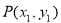 ,
,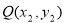 ,直线
,直线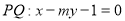 ,由
,由 ,消去
,消去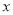 ,得
,得
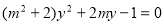 ,所以
,所以
设点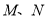 的坐标分别为
的坐标分别为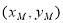 ,
,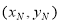 .
.
因为直线AP的方程为
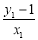
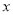 ,由
,由
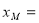
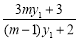 .
.
同理可得
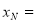
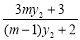
所以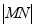
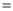
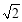
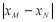

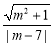
记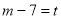 ,则
,则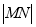
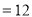
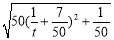 ,
,
当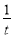 =-
=-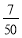 ,即
,即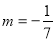 时,
时,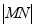 取最小值.
取最小值.
所以,当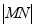 取最小值时
取最小值时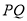 的方程为
的方程为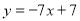 ,
,
考点:1.椭圆的标准方程,2.设而不求,联立方程组解题;3.弦长公式;4.求最值;

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 .若
.若 ,则集合
,则集合 可以是( ).
可以是( ). B.
B. C.
C. D.
D.
 的零点所在的区间是( )
的零点所在的区间是( ) B.
B. C.
C. D.
D.
 的棱长为1,
的棱长为1, 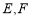 分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱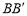 、
、 交于
交于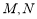 ,设
,设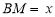 ,
, ,给出以下四个命题:
,给出以下四个命题:
 平面
平面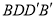 ;
;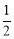 时,四边形
时,四边形 的面积最小;
的面积最小; 周长
周长 ,
, 是单调函数;
是单调函数;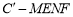 的体积
的体积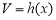 为常函数;
为常函数;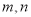 是两条不同的直线,
是两条不同的直线,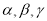 是三个不同的平面,给出下列命题,正确的是( )
是三个不同的平面,给出下列命题,正确的是( )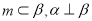 ,则
,则
 ,
,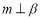 ,则
,则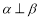
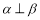 ,
, ,则
,则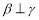
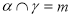 ,
, ,
,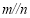 ,则
,则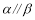 [
[ 成等差数列,点
成等差数列,点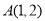 在动直线
在动直线 上的射影为
上的射影为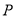 ,点Q在直线
,点Q在直线 上,则线段PQ长度的最小值是__________
上,则线段PQ长度的最小值是__________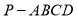 中,底面
中,底面 是菱形,
是菱形, 底面
底面 ,
, 是棱
是棱 上一点. 若
上一点. 若 ,则当
,则当 的面积为最小值时,直线
的面积为最小值时,直线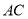 与平面
与平面 所成的角为( )
所成的角为( )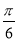 B.
B.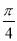 C.
C.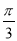 D.
D.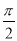
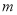 、
、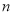 是两条不重合的直线,
是两条不重合的直线,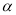 、
、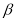 、
、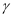 是三个两两不重合的平面,给出下列命题:
是三个两两不重合的平面,给出下列命题: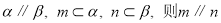 ;
;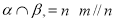 ,则
,则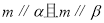
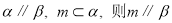 ;
;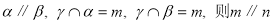 ;其中正确的命题是________
;其中正确的命题是________ ,
, ,记
,记
 在
在 处的切线方程;
处的切线方程; 在
在 上的最值.
上的最值.