题目内容
△ABC中,D为边BC上的一点,BD=33,sinB=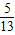 ,cos∠ADC=
,cos∠ADC= ,求AD.
,求AD.
【答案】分析:先由cos∠ADC= 确定角ADC的范围,因为∠BAD=∠ADC-B所以可求其正弦值,最后由正弦定理可得答案.
确定角ADC的范围,因为∠BAD=∠ADC-B所以可求其正弦值,最后由正弦定理可得答案.
解答:解:由cos∠ADC= >0,则∠ADC<
>0,则∠ADC<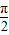 ,
,
又由知B<∠ADC可得B<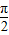 ,
,
由sinB=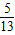 ,可得cosB=
,可得cosB=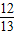 ,
,
又由cos∠ADC= ,可得sin∠ADC=
,可得sin∠ADC= .
.
从而sin∠BAD=sin(∠ADC-B)=sin∠ADCcosB-cos∠ADCsinB=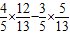 =
=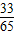 .
.
由正弦定理得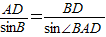 ,
,
所以AD=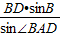 =
=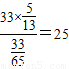 .
.
点评:三角函数与解三角形的综合性问题,是近几年高考的热点,在高考试题中频繁出现.这类题型难度比较低,一般出现在17或18题,属于送分题,估计以后这类题型仍会保留,不会有太大改变.解决此类问题,要根据已知条件,灵活运用正弦定理或余弦定理,求边角或将边角互化.
 确定角ADC的范围,因为∠BAD=∠ADC-B所以可求其正弦值,最后由正弦定理可得答案.
确定角ADC的范围,因为∠BAD=∠ADC-B所以可求其正弦值,最后由正弦定理可得答案.解答:解:由cos∠ADC=
 >0,则∠ADC<
>0,则∠ADC<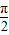 ,
,又由知B<∠ADC可得B<
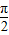 ,
,由sinB=
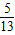 ,可得cosB=
,可得cosB=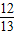 ,
,又由cos∠ADC=
 ,可得sin∠ADC=
,可得sin∠ADC= .
.从而sin∠BAD=sin(∠ADC-B)=sin∠ADCcosB-cos∠ADCsinB=
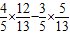 =
=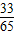 .
.由正弦定理得
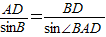 ,
,所以AD=
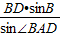 =
=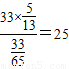 .
.点评:三角函数与解三角形的综合性问题,是近几年高考的热点,在高考试题中频繁出现.这类题型难度比较低,一般出现在17或18题,属于送分题,估计以后这类题型仍会保留,不会有太大改变.解决此类问题,要根据已知条件,灵活运用正弦定理或余弦定理,求边角或将边角互化.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
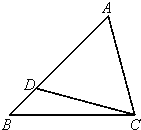 如图,在△ABC中,D为边AB上一点,DA=DC.已知B=
如图,在△ABC中,D为边AB上一点,DA=DC.已知B= ,∠ADB=120°,AD=2,若△ADC的面积为
,∠ADB=120°,AD=2,若△ADC的面积为 ,则∠BAC=( )
,则∠BAC=( ) ,则向量
,则向量 =( )。(用a,b表示)
=( )。(用a,b表示)