题目内容
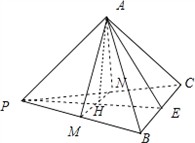
正三棱锥P﹣ABC中，M，N是侧棱PB、PC的中点，若截面AMN垂直于侧面PBC，求棱锥的侧面积与底面积的比．
解：取MN的中点H，连接PH交BC于E，连接AE、AH，
因为正三棱锥P﹣ABC中，所以PA=PB=PC，
M，N是侧棱PB、PC的中点，所以AH⊥MN，
截面AMN垂直于侧面PBC，所以BC⊥平面PAE，
∴AH是PE的垂直平分线．
所以，PA=AE
设PA=a，所以AB=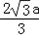
，
棱锥的侧面积为：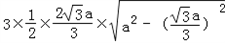
=
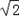a2．
底面面积为：
=
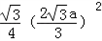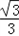a2．
棱锥的侧面积与底面积的比：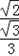
=
．
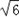因为正三棱锥P﹣ABC中，所以PA=PB=PC，
M，N是侧棱PB、PC的中点，所以AH⊥MN，
截面AMN垂直于侧面PBC，所以BC⊥平面PAE，
∴AH是PE的垂直平分线．
所以，PA=AE
设PA=a，所以AB=
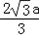，棱锥的侧面积为：
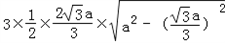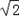=a2．底面面积为：
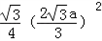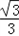=a2．棱锥的侧面积与底面积的比：
=．
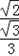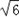练习册系列答案
相关题目
如图，在正三棱锥P-ABC中，M、N分别是侧棱PB、PC的中点，若截面AMN⊥侧面PBC，则此三棱锥的侧棱与底面所成角的正切值是．