题目内容
 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.分析:如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.设底面边长为2,侧棱长为a,通过解三角形的方法,解得a=
,设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,在△POB中求出 tan∠PBO.
| 3 |
解答:解: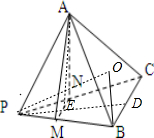 如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.
如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.
设底面边长为2,侧棱长为a,在△PBC中,PD2=a2-1,PE2=
PD2=
,ME=
MN=
.
在△PAB中,由余弦定理,cos∠APB=
=
,代入数据化简得
=
,AM2=
+2,
在△PAE中,由勾股定理,得出 PA2=AE2+PE2=AM2-ME2+PE2,即a2=
+2-
+
,解得a2=3,a=
设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,
在△POB中,BO=
,由勾股定理,PO2=PB2-BO2=
,PO=
,所以tan∠PBO=
=
,
三棱锥的侧棱与底面所成角的正切值是
.
故选C.
 如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.
如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.设底面边长为2,侧棱长为a,在△PBC中,PD2=a2-1,PE2=
| 1 |
| 4 |
| a2-1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
在△PAB中,由余弦定理,cos∠APB=
| PA2+PB2-AB2 |
| 2PB×PA |
| PA2+PM2-AM2 |
| 2PM×PA |
| a2-2 |
| a2 |
| ||
| a2 |
| a2 |
| 4 |
在△PAE中,由勾股定理,得出 PA2=AE2+PE2=AM2-ME2+PE2,即a2=
| a2 |
| 4 |
| 1 |
| 4 |
| a2-1 |
| 4 |
| 3 |
设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,
在△POB中,BO=
2
| ||
| 3 |
| 5 |
| 3 |
| ||
| 3 |
| PO |
| BO |
| ||
| 2 |
三棱锥的侧棱与底面所成角的正切值是
| ||
| 2 |
故选C.
点评:本题考查线面角的计算,线面垂直,面面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
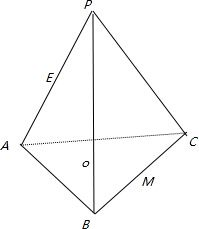 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP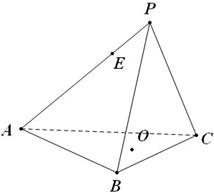 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
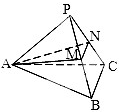
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP 如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )
如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )