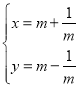题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的极大值为
的极大值为![]() ,无极小值;(2)
,无极小值;(2)![]() .
.
【解析】
(1)求出函数的导数,进而得到函数的单调性,然后可得函数的极值.(2)通过对参数![]() 的讨论得到函数的单调性,进而得到函数的最大值,然后将恒成立问题转化为
的讨论得到函数的单调性,进而得到函数的最大值,然后将恒成立问题转化为![]() ,解不等式可得所求范围.
,解不等式可得所求范围.
(1)当![]() 时,
时,![]() ,
,
∴![]() .
.
由![]() 得
得![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | 0 | - |
|
| 极大值 |
|
由表知,当![]() 时,函数
时,函数![]() 取得极大值,且极大值为
取得极大值,且极大值为![]() ,无极小值.
,无极小值.
(2)由题意得![]() .
.
①当![]() 时,则
时,则![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
∴对任意![]() ,
,![]() 不恒成立.
不恒成立.
②当![]() 时,
时,
则当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减.
单调递减.
∴当![]() 时,函数
时,函数![]() 取得极大值,也为最大值,且
取得极大值,也为最大值,且![]() .
.
∵不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,解得
,解得![]() .
.
综上可得实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某研究机构随机调查了![]() ,
,![]() 两个企业各100名员工,得到了
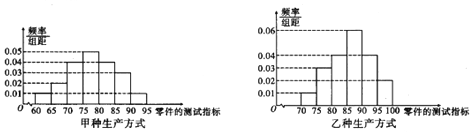
两个企业各100名员工,得到了![]() 企业员工收入的频数分布表以及
企业员工收入的频数分布表以及![]() 企业员工收入的统计图如下:
企业员工收入的统计图如下:
![]() 企业:
企业:
工资 | 人数 |
| 5 |
| 10 |
| 20 |
| 42 |
| 18 |
| 3 |
| 1 |
| 1 |
![]() 企业:
企业:

(1)若将频率视为概率,现从![]() 企业中随机抽取一名员工,求该员工收入不低于5000元的概率;
企业中随机抽取一名员工,求该员工收入不低于5000元的概率;
(2)(i)若从![]() 企业收入在
企业收入在![]() 员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,求这2人收入在
员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,求这2人收入在![]() 的人数
的人数![]() 的分布列.
的分布列.
(ii)若你是一名即将就业的大学生,根据上述调查结果,并结合统计学相关知识,你会选择去哪个企业就业,并说明理由.