题目内容
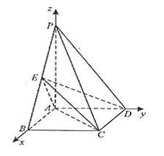
(本小题满分12分)如图,四棱锥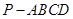 中,底面
中,底面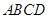 为矩形,
为矩形,
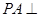 底面
底面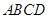 ,
,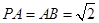 ,点
,点 是棱
是棱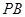 的中点.
的中点.
(1)证明: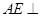 平面
平面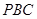 ;
;
(2)若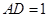 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 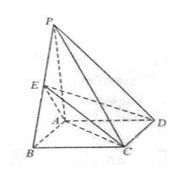
 中,底面
中,底面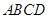 为矩形,
为矩形,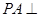 底面
底面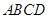 ,
,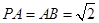 ,点
,点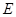 是棱
是棱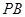 的中点.
的中点.(1)证明:
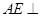 平面
平面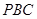 ;
;(2)若
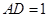 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 
(1)见解析;(2)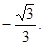
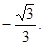
(1)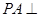 底面
底面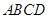
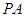 ⊥
⊥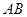
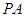 =
=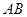
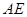 ⊥
⊥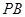 .
.
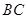 ⊥平面
⊥平面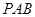
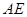 ⊥
⊥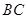 ,进而确定
,进而确定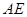 ⊥平面
⊥平面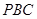 .
.
(2)解第(2)的关键是判断出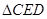 为等边三角形,
为等边三角形,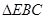 为等腰直角三角形,然后取
为等腰直角三角形,然后取 的中点
的中点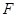 ,连接
,连接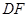 ,确定
,确定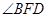 为所求的二面角的平面角.
为所求的二面角的平面角.
(1)证明:由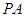 ⊥底面
⊥底面 ,得
,得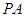 ⊥
⊥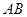 ,由
,由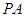 =
=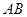 知
知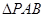 为等腰直角三角形,又点
为等腰直角三角形,又点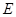 是棱
是棱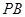 的中点,故
的中点,故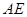 ⊥
⊥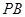 由题意知
由题意知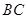 ⊥
⊥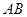 ,又
,又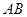 是
是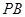 在面
在面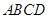 内的射影,由三垂线定理得
内的射影,由三垂线定理得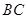 ⊥
⊥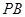 ,从而
,从而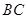 ⊥平面
⊥平面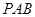 ,因
,因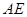 ⊥
⊥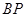 ,
,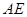 ⊥
⊥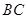 ,所以
,所以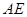 ⊥平面
⊥平面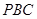 .
.
(2)解:由(1)知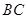 ⊥平面
⊥平面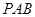 ,又
,又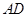 //
//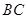 ,得
,得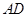 ⊥平面
⊥平面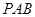 ,故
,故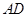 ⊥
⊥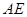 .
.
在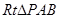 中,
中,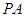 =
=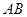 =
=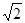 ,
,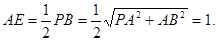
从而在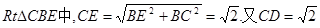 ,所以
,所以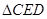 为等边三角形,
为等边三角形,
取 的中点
的中点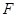 ,连接
,连接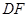 ,则
,则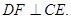
因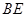 =
=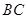 =1,且
=1,且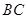 ⊥
⊥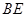 ,则
,则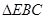 为等腰直角三角形,连接
为等腰直角三角形,连接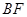 ,则
,则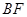 ⊥
⊥ ,
,
所以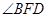 为所求的二面角的平面角.
为所求的二面角的平面角.
连接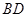 ,在
,在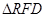 中,
中,
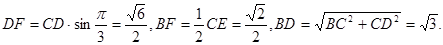
所以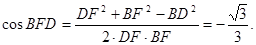 故二面角
故二面角 的平面角的余弦值为
的平面角的余弦值为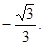
解二:(1)如图,以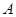 为坐标原点,射线
为坐标原点,射线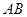 、
、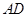 、
、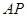 分别为
分别为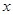 轴、
轴、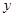 轴、
轴、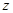 轴正半轴,建立空间直角坐标系.
轴正半轴,建立空间直角坐标系.
设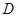
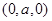 ,则
,则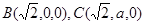
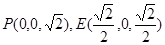 .
.
于是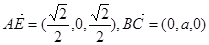 ,
, 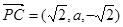
则 ,所以
,所以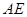 ⊥平面
⊥平面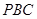 .
.
(2)解:设平面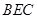 的法向量为
的法向量为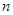 ,由(1)知,
,由(1)知,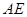 ⊥平面
⊥平面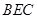 ,
,
故可取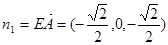
设平面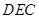 的法向量
的法向量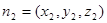 ,则
,则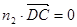 ,
,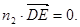
由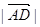 =1,得
=1,得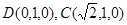 从而
从而
故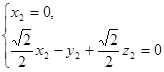 所以
所以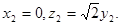 可取
可取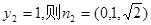
从而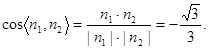 所以二面角
所以二面角 的平面角的余弦值为
的平面角的余弦值为
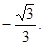

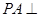 底面
底面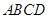
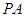 ⊥
⊥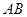
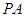 =
=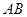
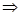
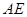 ⊥
⊥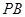 .
.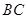 ⊥平面
⊥平面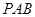
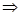
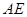 ⊥
⊥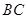 ,进而确定
,进而确定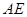 ⊥平面
⊥平面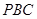 .
.(2)解第(2)的关键是判断出
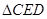 为等边三角形,
为等边三角形,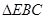 为等腰直角三角形,然后取
为等腰直角三角形,然后取 的中点
的中点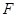 ,连接
,连接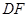 ,确定
,确定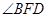 为所求的二面角的平面角.
为所求的二面角的平面角.
(1)证明:由
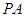 ⊥底面
⊥底面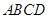 ,得
,得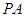 ⊥
⊥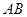 ,由
,由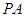 =
=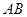 知
知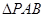 为等腰直角三角形,又点
为等腰直角三角形,又点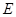 是棱
是棱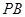 的中点,故
的中点,故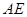 ⊥
⊥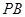 由题意知
由题意知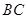 ⊥
⊥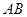 ,又
,又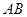 是
是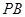 在面
在面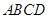 内的射影,由三垂线定理得
内的射影,由三垂线定理得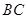 ⊥
⊥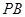 ,从而
,从而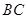 ⊥平面
⊥平面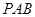 ,因
,因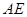 ⊥
⊥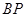 ,
,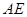 ⊥
⊥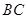 ,所以
,所以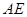 ⊥平面
⊥平面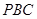 .
.(2)解:由(1)知
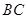 ⊥平面
⊥平面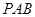 ,又
,又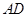 //
//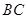 ,得
,得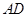 ⊥平面
⊥平面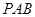 ,故
,故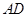 ⊥
⊥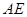 .
.在
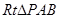 中,
中,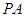 =
=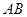 =
=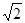 ,
,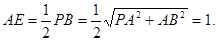
从而在
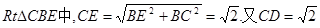 ,所以
,所以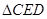 为等边三角形,
为等边三角形,取
 的中点
的中点 ,连接
,连接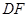 ,则
,则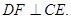
因
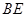 =
=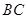 =1,且
=1,且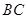 ⊥
⊥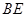 ,则
,则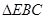 为等腰直角三角形,连接
为等腰直角三角形,连接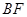 ,则
,则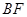 ⊥
⊥ ,
,所以
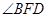 为所求的二面角的平面角.
为所求的二面角的平面角.连接
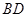 ,在
,在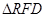 中,
中,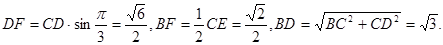
所以
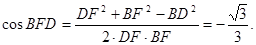 故二面角
故二面角 的平面角的余弦值为
的平面角的余弦值为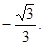
解二:(1)如图,以
 为坐标原点,射线
为坐标原点,射线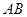 、
、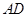 、
、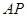 分别为
分别为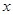 轴、
轴、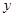 轴、
轴、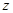 轴正半轴,建立空间直角坐标系.
轴正半轴,建立空间直角坐标系.设
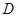
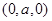 ,则
,则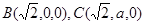
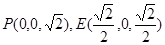 .
.于是
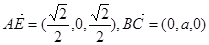 ,
, 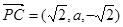
则
 ,所以
,所以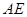 ⊥平面
⊥平面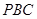 .
.(2)解:设平面
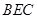 的法向量为
的法向量为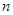 ,由(1)知,
,由(1)知,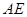 ⊥平面
⊥平面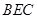 ,
,故可取
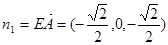
设平面
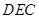 的法向量
的法向量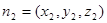 ,则
,则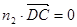 ,
,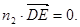
由
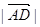 =1,得
=1,得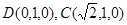 从而
从而
故
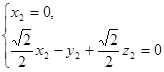 所以
所以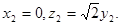 可取
可取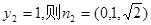
从而
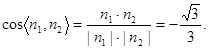 所以二面角
所以二面角 的平面角的余弦值为
的平面角的余弦值为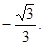


练习册系列答案
相关题目

 中,
中,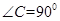 ,D,E分别为AC,AB的中点,点F为线段CD上的一点,将
,D,E分别为AC,AB的中点,点F为线段CD上的一点,将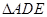 沿DE折起到
沿DE折起到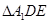 的位置,使
的位置,使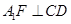 ,如图2.
,如图2.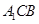
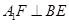
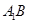 上是否存在点Q,使
上是否存在点Q,使 ?说明理由。
?说明理由。
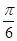 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD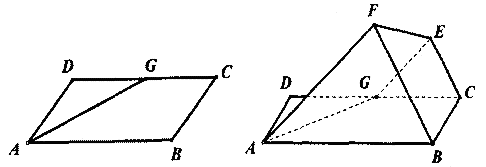
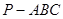 中,
中,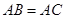 ,
,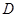 为
为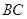 的中点,
的中点,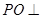 平面
平面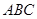 ,垂足
,垂足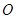 落在线段
落在线段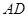 上,已知
上,已知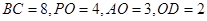 。
。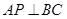 ;
;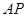 上是否存在点M,使得二面角
上是否存在点M,使得二面角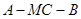 为直二面角?若存在,求
为直二面角?若存在,求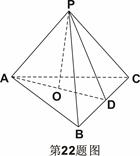
 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
 、
、 、
、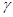 和直线
和直线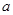 、
、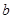 、
、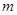 、
、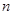 ,下列命题中真命题是( )
,下列命题中真命题是( )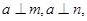
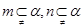 ,则
,则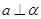 ;
;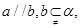 则
则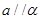 ;
;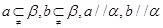 ,则
,则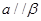 ;
;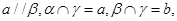 则
则 .
. 处,同一时刻,一个长
处,同一时刻,一个长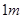 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为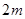 ,则该球的半径等于( )
,则该球的半径等于( )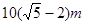

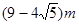
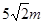
 A
A AOB和
AOB和