题目内容
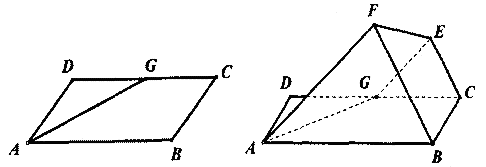
如图,己知平行四边形ABCD中,∠ BAD = 600,AB=6, AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG。
(I)求证:直线CE//平面ABF;
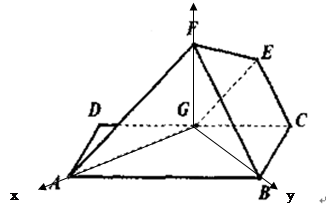
(II)如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值.
(Ⅲ)若直线AF与平面 ABCD所成角为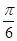 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD
(I)求证:直线CE//平面ABF;
(II)如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值.
(Ⅲ)若直线AF与平面 ABCD所成角为
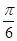 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD
(1)见解析;(2)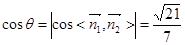 ;(3)见解析.
;(3)见解析.
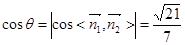 ;(3)见解析.
;(3)见解析.第一问中利用线面平行的判定定理 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF
CE//平面ABF
第二问中,因为AG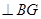 ,如图建立空间直角坐标系
,如图建立空间直角坐标系
(1)证明: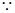 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF
 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF …………4分
CE//平面ABF …………4分
(2)AG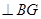 ,如图建立空间直角坐标系
,如图建立空间直角坐标系
设平面BFEC的法向量为 则
则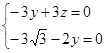
 平面AEF的法向量
平面AEF的法向量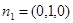

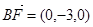
,利用数量积的公式得到二面角的表示。
第三问中,
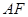 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)
又FG=GB=3
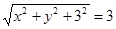

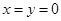
 F(0,0,3)
F(0,0,3)
 GF=(0,0,3)
GF=(0,0,3) GF
GF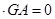
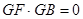

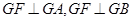

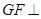 平面ABCD
平面ABCD
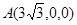
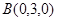
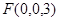
 平面AEF的法向量
平面AEF的法向量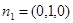

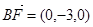
设平面BFEC的法向量为 则
则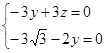

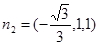

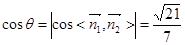 即为所求。……………10分
即为所求。……………10分
(3)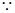
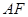 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)
又FG=GB=3
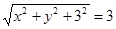

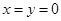
 F(0,0,3)
F(0,0,3)
 GF=(0,0,3)
GF=(0,0,3) GF
GF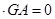
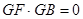

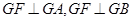

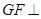 平面ABCD…………15分
平面ABCD…………15分
 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF
CE//平面ABF第二问中,因为AG
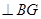 ,如图建立空间直角坐标系
,如图建立空间直角坐标系(1)证明:
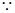 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF …………4分
CE//平面ABF …………4分(2)AG
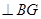 ,如图建立空间直角坐标系
,如图建立空间直角坐标系设平面BFEC的法向量为
 则
则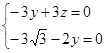
 平面AEF的法向量
平面AEF的法向量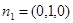

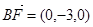
,利用数量积的公式得到二面角的表示。
第三问中,
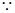
 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)又FG=GB=3

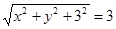

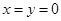
 F(0,0,3)
F(0,0,3) GF=(0,0,3)
GF=(0,0,3) GF
GF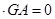
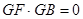

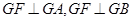

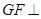 平面ABCD
平面ABCD
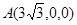
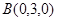
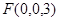
 平面AEF的法向量
平面AEF的法向量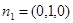

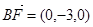
设平面BFEC的法向量为
 则
则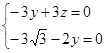

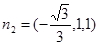

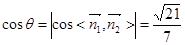 即为所求。……………10分
即为所求。……………10分(3)
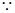
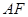 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)又FG=GB=3

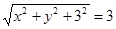

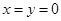
 F(0,0,3)
F(0,0,3) GF=(0,0,3)
GF=(0,0,3) GF
GF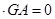
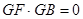

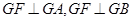

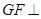 平面ABCD…………15分
平面ABCD…………15分
练习册系列答案
相关题目
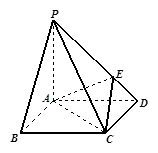
 的正方形,且PD=
的正方形,且PD=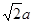 .
.
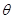 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.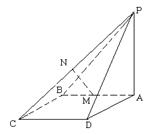
 中,底面
中,底面 为矩形,
为矩形, 底面
底面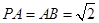 ,点
,点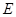 是棱
是棱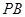 的中点.
的中点.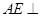 平面
平面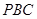 ;
;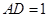 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 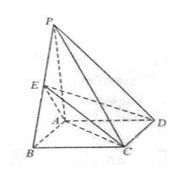
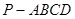 中,平面
中,平面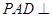 平面
平面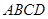 ,
,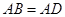 ,
,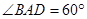 ,
,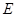 、
、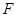 分别是
分别是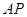 、
、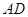 的中点。
的中点。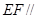 平面
平面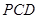 ;
;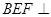 平面
平面 。(12分)
。(12分)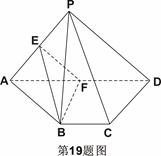
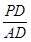 =
=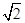 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.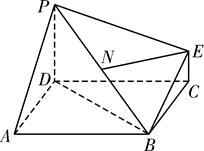
 中,
中, ,
, ,点
,点 在棱
在棱 上移动,问
上移动,问 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.
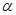 和共面
和共面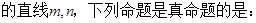 ( )
( )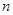
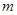 ∥
∥