题目内容
 某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a(
某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a( ),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计)
),且前轮E已在BC段上时,后轮中心在F位置;若前轮中心到达G处时,后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在E和G处时与地面的接触点分别为S和T,且BS=60cm,ST=100cm.(其它因素忽略不计)
(1)如图(2)所示,FH和GE的延长线交于点O,求证:OE=40cot (cm);
(cm);
(2)当a= π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
π时,后轮中心从F处移动到H处实际移动了多少厘米?(精确到1cm)
 解:(1)由OE∥BC,OH∥AB,得∠EOH=α,…..(2分)
解:(1)由OE∥BC,OH∥AB,得∠EOH=α,…..(2分)过点B作BM⊥OE,BN⊥OH,则
Rt△OMB
 Rt△ONB,从而∠BOM=
Rt△ONB,从而∠BOM= .…..(4分)
.…..(4分)在Rt△OMB中,由BM=40得OM=40cot
 ,从而,OE=OM+ME=OM+BS=40cot
,从而,OE=OM+ME=OM+BS=40cot +60.…..(6分)
+60.…..(6分)(2)由(1)结论得OE=
 +60.
+60.设OH=x,OF=y,在△OHG中,由余弦定理得,
2802=x2+(
 +60+100)2-2x(
+60+100)2-2x( +60+100)cos150°,
+60+100)cos150°,解得x≈118.8cm.…..(9分)
在△OEF中,由余弦定理得,
2802=y2+(
 +60)2-2y(
+60)2-2y( +60)cos150°,
+60)cos150°,解得y≈216.5cm.…..(12分)
所以,FH=y-x≈98cm,
即后轮中心从F处移动到H处实际移动了约98cm.…(14分)
分析:(1)依题意,∠EOH=α,由Rt△OMB
 Rt△ONB,可求得∠BOM=
Rt△ONB,可求得∠BOM= ,在Rt△OMB中,可求得OM=40cot
,在Rt△OMB中,可求得OM=40cot ,从而可证得结论;
,从而可证得结论;(2)由(1)结论得OE=
 +60,设OH=x,OF=y,在△OHG中,由余弦定理可求得x,在△OEF中,由余弦定理可求得y,而FH=y-x,从而可得答案.
+60,设OH=x,OF=y,在△OHG中,由余弦定理可求得x,在△OEF中,由余弦定理可求得y,而FH=y-x,从而可得答案.点评:本题考查余弦定理,考查根据实际问题选择函数类型,着重考查分析理解与运算能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
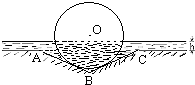 (2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).
(2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).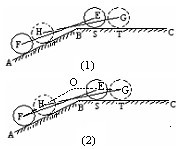 (2013•徐汇区一模)某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a(
(2013•徐汇区一模)某种型号汽车四个轮胎半径相同,均为R=40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为l=280cm (假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC(如图(1)所示,其中∠ABC=a( ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路 (如图(1)所示,其中
(如图(1)所示,其中 (
(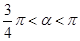 )),且前轮
)),且前轮 已在
已在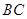 段上时,后轮中心在
段上时,后轮中心在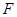 位置;若前轮中心到达
位置;若前轮中心到达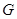 处时,后轮中心在
处时,后轮中心在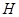 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和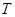 ,且
,且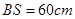 ,
,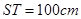 . (其它因素忽略不计)
. (其它因素忽略不计)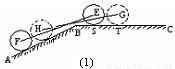
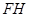 和
和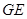 的延长线交于点
的延长线交于点 ,
,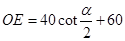 (cm);
(cm);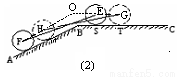
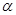 =
=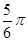 时,后轮中心从
时,后轮中心从 ,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑
,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑 形成顶角为
形成顶角为 的等腰三角形,且
的等腰三角形,且 ,如果地面上有
,如果地面上有 (
( )高的积水(此时坑内全是水,其它因素忽略不计).
)高的积水(此时坑内全是水,其它因素忽略不计). 、
、 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为 ;
; 的最大值.
的最大值.