题目内容
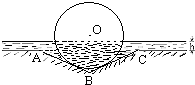 (2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).
(2012•徐汇区一模)某种型号汽车的四个轮胎半径相同,均为R=40cm,该车的底盘与轮胎中心在同一水平面上.该车的涉水安全要求是:水面不能超过它的底盘高度.如图所示:某处有一“坑形”地面,其中坑ABC形成顶角为120°的等腰三角形,且AB=BC=60cm,如果地面上有h(cm)(h<40)高的积水(此时坑内全是水,其它因素忽略不计).(1)当轮胎与AB、BC同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为d=10+
80
| ||
| 3 |
(2)假定该汽车能顺利通过这个坑(指汽车在过此坑时,符合涉水安全要求),求h的最大值.(精确到1cm).
分析:(1)设轮胎与AB边的切点为T,轮胎中心为O,则|OT|=40,由∠ABC=120°,知∠OBT=60°,可得OB|=
,由此求得从B点到轮胎最上部的距离.
(2)由题意可得只要d≥40,即
+10-h≥4040,由此求得h的最大值.
| 2×40 | ||
|
(2)由题意可得只要d≥40,即
| 80 | ||
|
解答:解:(1)当轮胎与AB、BC同时接触时,设轮胎与AB边的切点为T,轮胎中心为O,则|OT|=40,
由∠ABC=120°,知∠OBT=60°,…..(2分)
故|OB|=
..…..(4分)
所以,从B点到轮胎最上部的距离为
+40,…..(6分)
此轮胎露在水面外的高度为d=
+40-(60cos60°+h)=
+10-h,得证.…..(8分)
(2)只要d≥40,…..(12分)
即
+10-h≥4040,解得h≤16cm,
所以h的最大值为16cm.…..(14分)
由∠ABC=120°,知∠OBT=60°,…..(2分)
故|OB|=
| 2×40 | ||
|
所以,从B点到轮胎最上部的距离为
| 2×40 | ||
|
此轮胎露在水面外的高度为d=
| 2×40 | ||
|
| 80 | ||
|
(2)只要d≥40,…..(12分)
即
| 80 | ||
|
所以h的最大值为16cm.…..(14分)
点评:本题主要考查直线和圆的位置关系,函数的最值及其几何意义,属于中档题.

练习册系列答案
相关题目